Bookstall

paper - 2023-05-02：论文速递

Wiki paper

2023-05-02：论文速递

1、Are Emergent Abilities of Large Language Models a Mirage?

大型语言模型的涌现能力是种幻觉吗？

《Are Emergent Abilities of Large Language Models a Mirage?》

  • URL：https://arxiv.org/abs/2304.15004

  • Official Code：

  • 单位：斯坦福大学

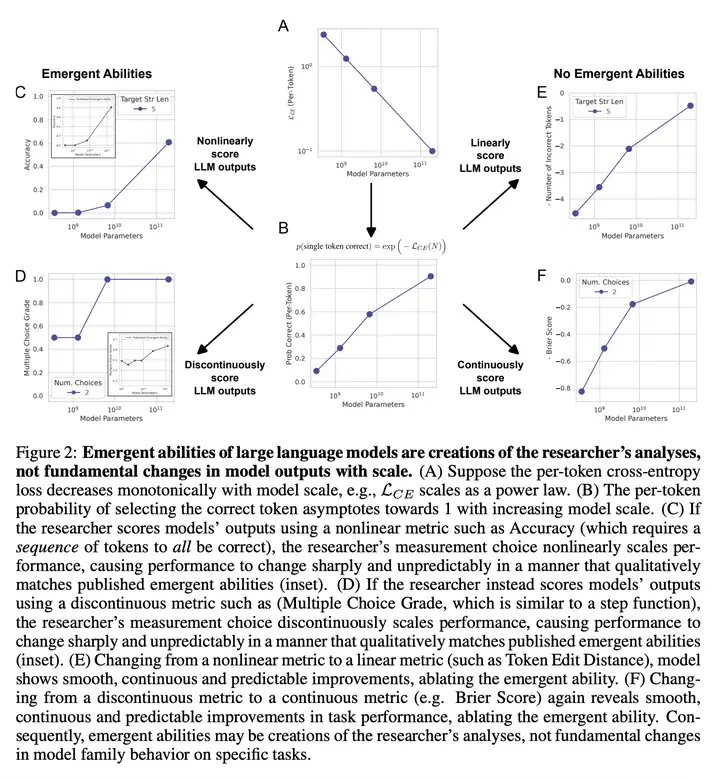
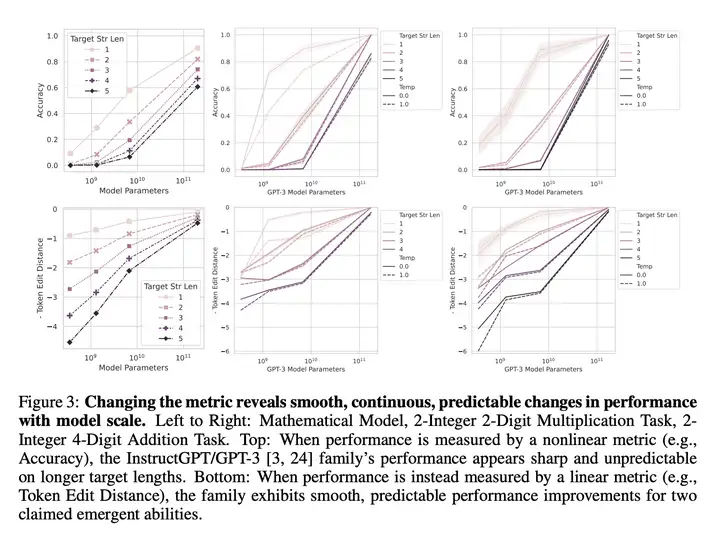
之前的研究表明，大型语言模型表现出的涌现能力具有两个特点：突然出现和不可预测性。本研究旨在提出另一种解释，以探讨这种现象背后的原因，从而更好地理解大型语言模型的行为。具体来说，作者认为：大型语言模型所表现出的涌现能力并非模型行为在特定任务和特定模型族下的基本变化，而是研究人员分析时 选择的度量方式 所导致的结果。通过对固定模型输出进行分析，可以选择一种度量方式来推断出涌现能力，也可以选择另一种度量方式来消除涌现能力。

研究通过简单的数学模型进行解释，然后以三种互补的方式进行测试，并在多个实验中进行了验证。结果表明，涌现能力可能不是 AI 模型规模扩展的基本特性。

2、PMC-LLaMA: Further Finetuning LLaMA on Medical Papers

PMC-LLaMA: 用医学论文进一步微调 LLaMA

《PMC-LLaMA: Further Finetuning LLaMA on Medical Papers》

  • URL：https://arxiv.org/abs/2304.14454

  • Official Code：https://github.com/chaoyi-wu/pmc-llama

  • 单位：上海交通大学，上海人工智能实验室

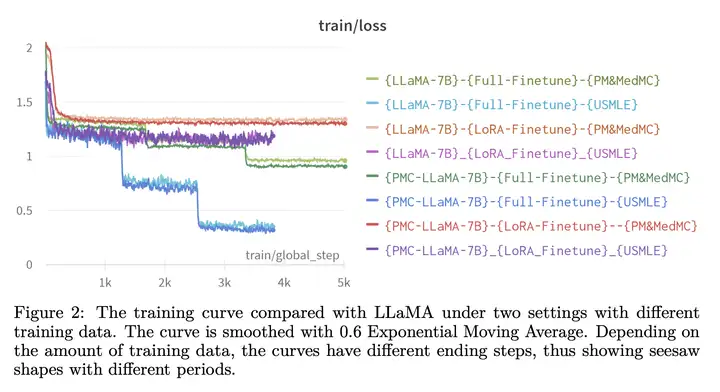
PMC-LlaMA 训练过程

PMC-LLaMA 训练过程的示意图如下所示：

PMC-LLaMA 训练过程的示意图

实验结果

PMC-LLaMA 的训练 Loss

3、LLaMA-Adapter V2: Parameter-Efficient Visual Instruction Model

LLaMA-Adapter V2: 参数高效的视觉指令模型

《LLaMA-Adapter V2: Parameter-Efficient Visual Instruction Model》

  • URL：https://arxiv.org/abs/2304.15010

  • Official Code：https://github.com/ZrrSkywalker/LLaMA-Adapter

  • 单位：上海人工智能实验室、香港中文大学

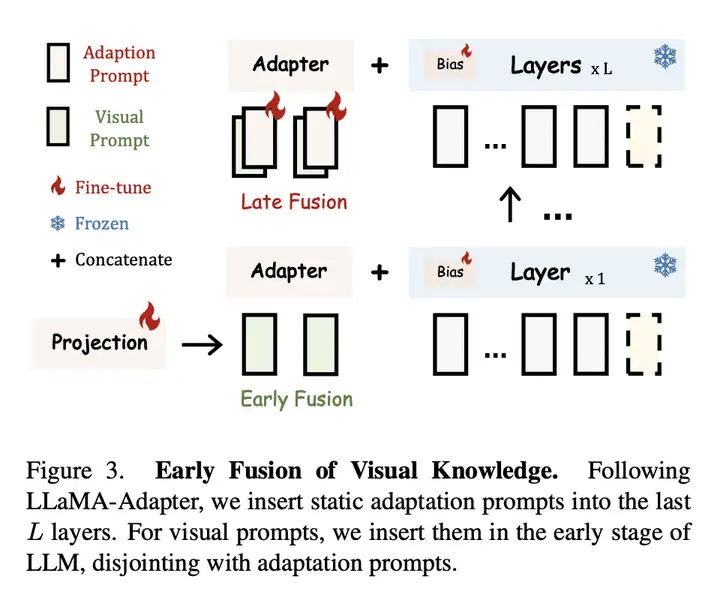
LLaMA-Adapter V2 训练过程的示意图如下所示：

LLaMA-Adapter V2 训练过程的示意图

更多

1、An Empirical Study of Multimodal Model Merging

多模态模型合并的实证研究

《An Empirical Study of Multimodal Model Merging》

  • URL：https://arxiv.org/abs/2304.14933

  • Official Code：https://github.com/ylsung/vl-merging

  • 单位：UNC Chapel Hill、Microsoft

模型合并（例如，通过插值或任务算法）融合在不同任务上训练的多个模型以生成 多任务解决方案。

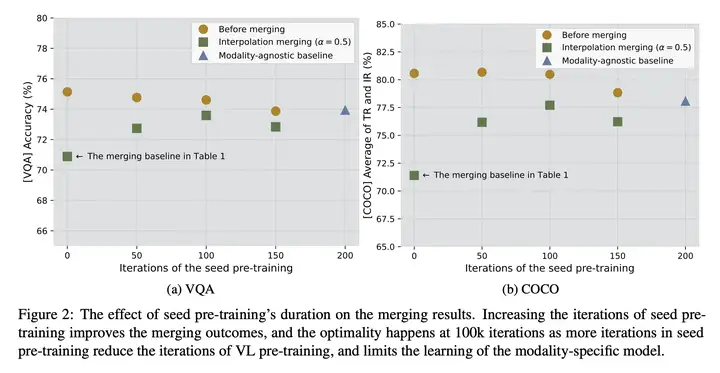
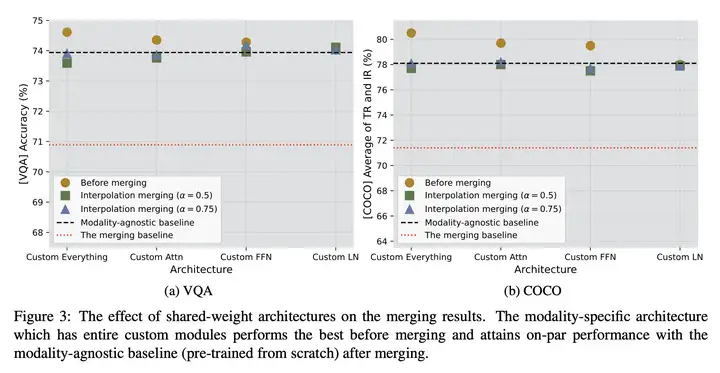
  • 动机：之前的研究表明，模型合并技术在训练相似任务且使用相同初始化的模型方面非常成功。本研究将这种技术扩展到多模态场景，并研究了如何将模态特定的模型转换为模态不可知的模型。

  • 方法：通过合并不同模态下的 Transformer 模型，创建了一个参数高效的、模态不可知（modality-agnostic）的多模态体系结构，并系统地探讨了影响模型合并后性能的 关键因素，包括 初始化、合并机制和模型架构。

  • 优势：通过使用 模型合并技术，显著提高了模态特定模型的性能，使其 接近或甚至超过了从头开始预训练的模态不可知基准模型。这为 多模态任务 的解决提供了一种有效的解决方案。

模型合并的框架

多模态模型合并（multimodal merging）的框架示意图如下所示：

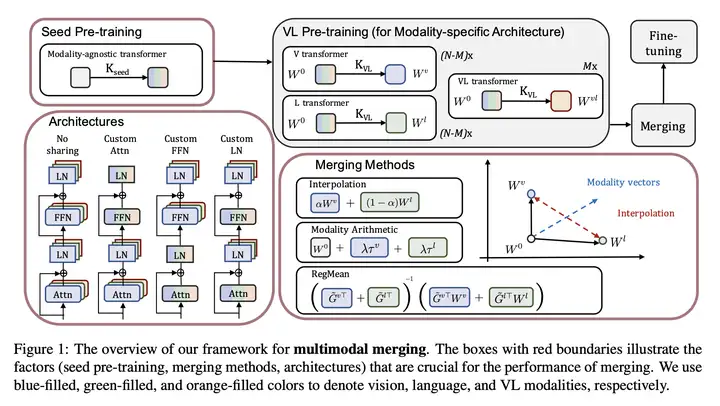
多模态模型合并的框架示意图

其中，红色框表示的是影响合并之后模型性能的因素，包括初始的 Seed Pre-training 模型、模型合并的架构、模型合并的方式。蓝色、绿色和橙色分别表示 vision 模态、language 模态和 vision-language (VL) 模态。

模型合并的架构包括：

  • No Sharing：每个模态的模型的 Attn、FFN、LN 都是单独进行的

  • Custom Attn：只有 Attn 和后面跟着的 LN 是单独进行的

  • Custom FFN：只有 FFN 和后面跟着的 LN 是单独进行的

  • Custom LN：只有 LN 是单独进行的

模型合并的方式包括：

  • Interpolation（插值）

  • Modality Arithmetic

  • RegMean

实验结果

2、ResiDual: Transformer with Dual Residual Connections

ResiDual：基于双残差连接的 Transformer

《ResiDual: Transformer with Dual Residual Connections》

  • URL：https://arxiv.org/abs/2304.14802

  • 单位：Microsoft Research

  • Official Code：https://github.com/microsoft/ResiDual

  • 动机：Transformer 网络由于其卓越的性能已经成为许多任务的首选架构，但如何在 Transformer 中实现残差连接仍然存在争议。

  • 方法：提出一种名为 ResiDual 的 Transformer 架构，通过利用前置层归一化和后置层归一化的双残差连接机制，在解决 Post-LN 和 Pre-LN 变体中存在的梯度消失和表示坍缩问题的同时，取得了更好的机器翻译性能。

  • 优势：ResiDual 结构融合了 Post-LN 和 Pre-LN 变体的优点，避免了它们的局限性，同时具有更好的理论分析和实验结果，可作为不同 AI 模型(如大型语言模型)的基础架构。

前言

While both variants enjoy their advantages, they also suffer from severe limitations:

  • Post-LN causes gradient vanishing issue（梯度消失问题） that hinders training deep Transformers

  • Pre-LN causes representation collapse issue（表示崩溃问题） that limits model capacity

In this paper, we propose ResiDual, a novel Transformer architecture with Pre-Post-LN (PPLN), which fuses the connections in Post-LN and Pre-LN together, and inherits their advantages while avoids their limitations.

提出了一种新的 Transformer 结构：ResiDual，将 Post-LN 和 Pre-LN 结合在一起，即 Pre-Post-LN（PPLN），继承了两者的优点，并避免了它们的局限性。

实验结果：Residual 在不同网络深度和数据大小的多个 机器翻译基准测试 中优于 Post-LN 和 Pre-LN。

由于良好的理论和实验性能，Residual Transformer 可以作为不同 AI 模型（例如，大型语言模型）的基础架构。

Post-LN

给定一个有 \(N\) 个残差块的 Post-LN Transformer，并且输出的形状是 \(R^{n\times d}\)，其中 \(n\) 表示序列长度，\(d\) 表示嵌入维度。

  • \(\overrightarrow{x}\in R^{n\times d}\) 表示整个序列

  • \(x\in R^{d}\) 表示序列的一个元素

  • \(\overrightarrow{x}^a\in R^{n\times d}\) 表示经过 addition 操作之后的 tensor

  • \(\overrightarrow{x}^a_k\in R^{n\times d}\) 表示经过第 \(k\) 个残差块的 addition 操作之后的 tensor

  • \(\overrightarrow{x}^{ln}_k\in R^{n\times d}\) 表示经过第 \(k\) 个残差块的 LN 操作之后的 tensor

  • \(\overrightarrow{x}^f_k\in R^{n\times d}\) 表示经过第 \(k\) 个残差块的 \(f(\cdot; w_k)\) 操作之后的 tensor

    • 其中，\(f(\cdot; w_k)\) 可以是 Self-Attention、Cross-Attention、FFN
\[\begin{align} \boldsymbol{x}_k^a&=\boldsymbol{x}_k^{ln}+\boldsymbol{x}_k^f=\boldsymbol{x}_k^{ln}+f_k(\overrightarrow{\boldsymbol{x}}_k^{ln}\boldsymbol{w}_k) \\ \quad\boldsymbol{x}_{k+1}^{ln}&=\operatorname{LN}(\boldsymbol{x}_k^a) \\ \end{align}\]

Pre-LN 模型最终的输出为：

\[y = LN(\boldsymbol{x}_{N+1}^a) = LN(\sum_{k=1}^N \boldsymbol{x}_k^f)\]

直觉上，\(x_k^f\) 会被归一化 \(N-k\) 次，对应的权重 \(w_k\) 的梯度也相应的会被归一化 \(N-k\) 次。因此，在反向传播时，梯度从深层网络传递回浅层网络时，会呈 指数下降，最终导致 梯度消失（Gradient Vanish）。

直觉上，这种 不平衡的梯度 会阻碍模型训练。因此，在实际使用时，学习率预热等训练技巧对于训练 Post-LN 模型是必要的。

Pre-LN

\[\begin{align} \boldsymbol{x}_k^{ln}&=\operatorname{LN}(\boldsymbol{x}_k^a) \\ \quad\boldsymbol{x}_{k+1}^a&=\boldsymbol{x}_k^a+\boldsymbol{x}_k^f=\boldsymbol{x}_k^a+f_k(\overrightarrow{\boldsymbol{x}}_k^{ln};\boldsymbol{w}_k) \end{align}\]

Post-LN 模型最终的输出为：

\[y = x_{N+1}^{ln} = LN(x_N^a)\]

\(x_k^f\) 只会被归一化一次，在前向和后向传播时不会因为被 \(LN\) 阻塞，因此 Pre-LN 不存在梯度消失。

但是，Pre-LN 会导致另一个问题：表示坍塌（representation collapse，模式坍塌）。

  • 这意味着后面的块 \(x_k^f\) 的输出对 \(x_k^a\) 的总方差几乎没有贡献

  • 并且这个问题可能会限制模型的容量

ResiDual 结构

ResiDual 的结构示意图如下所示：

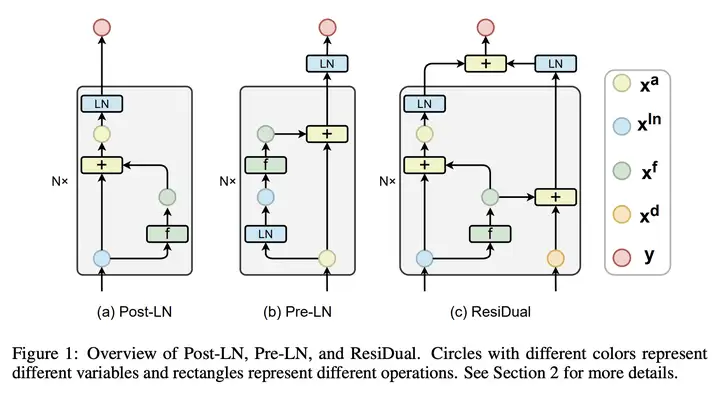
ResiDual 结构示意图

其中，每种不同颜色的圈表示不同的变量，不同颜色的矩形表示不同的操作。

具体来说，左分支的计算过程如下：

\[\begin{align} \boldsymbol{x}_k^a&=\boldsymbol{x}_k^{ln}+\boldsymbol{x}_k^f=\boldsymbol{x}_k^{ln}+f_k(\overrightarrow{\boldsymbol{x}}_k^{ln};\boldsymbol{w}_k) \\ \quad\boldsymbol{x}_{k+1}^{ln}&=\operatorname{LN}(\boldsymbol{x}_k^a) \\ \end{align}\]

右分支的计算过程如下：

\[\begin{align} \boldsymbol{x}_{k+1}^d = \boldsymbol{x}_k^d + \boldsymbol{x}_k^f \end{align}\]

其中，\(\boldsymbol{x}_k^d \in R^{n\times d}\)，表示 dual residual tensor（类似 Pre-LN 的 \(\boldsymbol{x}^a\)）。

最终，将左分支和右分支的结果进行相加，得到 ResiDual 模型的输出为：

\[y = \boldsymbol{x}_{N+1}^{ln} + LN(x_{N+1}^d)\]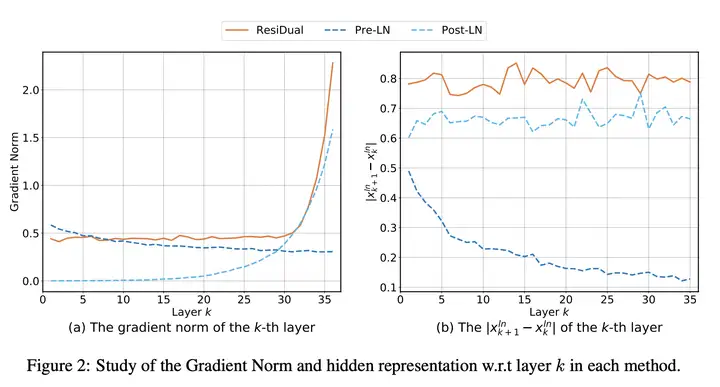

参考

文档信息

Search

    Table of Contents