量化定义

假设神经网络有 L 个具有可学习参数的层，表示为 {W1, W2, …, WL}，其中 θ 表示所有这些参数的组合。不失一般性，我们关注监督学习问题，其名义目标是优化以下经验风险最小化函数：

其中 \((x, y)\) 是输入数据和相应的标签，\(l(x, y; θ)\) 是损失函数（例如均方误差或交叉熵损失），\(N\) 是数据点的总数。我们还将第 \(i\) 层的输入隐藏激活表示为 \(h_i\)，并将相应的输出隐藏激活表示为 \(a_i\)。我们假设我们有经过训练的模型参数 \(\theta\)，以浮点精度存储。在量化中，目标是将参数 (θ) 以及中间激活映射（即 \(h_i\)、\(a_i\)）的精度降低到低精度，同时对模型的泛化能力/精度影响最小。为此，我们需要定义一个量化运算符，将浮点值映射到量化值，如下所述。

基础量化方法：

• 均匀 VS 非均匀：生成的量化值（也称为量化级别）是否为均匀间隔的

获取浮点实数，并将它们映射到较低精度范围，如图 1 所示。主流的量化函数如下：

其中，\(Q\) 表示量化运算符，\(r\) 是实值输入（激活或权重），\(S\) 是实值缩放因子，\(Z\) 是整数零点。

可以通过通常称为 反量化（dequantization） 的操作从量化值 \(Q(r)\) 恢复实际值 \(r\)：

注意：由于舍入操作，恢复的实际值 ̃\(\hat{r}\) 将不完全匹配 \(r\)（有损压缩）。

• 对称 VS 非对称：确定截断的范围（How）

均匀量化的一个重要因素是等式中缩放因子 \(S\) 的选择，该比例因子实质上将给定范围的实值 \(r\) 划分为多个分区：

其中 \([α, β]\) 表示裁剪范围，即我们裁剪真实值的有界范围，\(b\) 是量化位宽。

因此，为了确定缩放因子 \(S\)，我们需要首先确定裁剪范围 \([\alpha, \beta]\)。

选择限幅范围的过程通常称为 校准（calibration）。

一个简单的选择是使用信号的 min/max 作为限幅范围，即 \(α = r_{min}\)，\(β = r_{max}\)。这种方法是一种 非对称量化 方案，因为限幅范围不一定相对于原点对称，即 \(-α \neq β\)，如下图（右）所示。

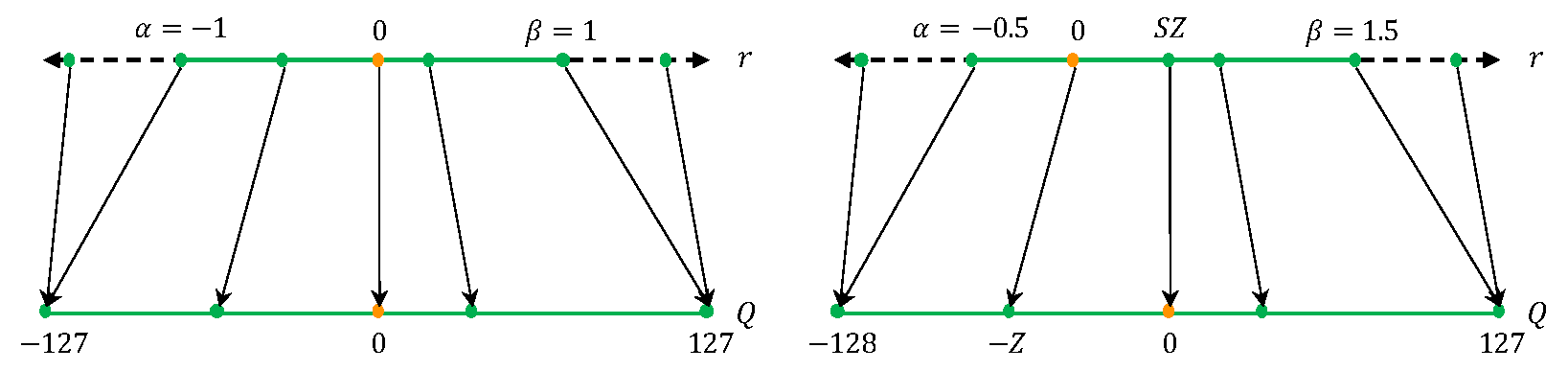
一种流行的对称量化方法是：

与对称量化相比，非对称量化通常会导致更严格的裁剪范围。当目标权重或激活不平衡时（例如，ReLU 之后的激活始终具有非负值），这一点尤其重要。然而，使用对称量化可以简化量化函数，将零点替换为 \(Z = 0\)：

在对称量化中，缩放因子 \(S\) 有两种选择方式：

• full range：\(S = \frac{2\max{(r)}}{2^b - 1}\)

  • full INT8 range：[-128, 127]

• restricted range：\(S = \frac{\max{(r)}}{2^{b-1} - 1}\)

  • full INT8 range：[-127, 127]

• 范围校准算法：动态 VS 非动态（When）

到目前为止，我们讨论了确定 \([α, β]\) 削波范围的不同校准方法。量化方法的另一个重要区别在于限幅范围 何时确定。

这个范围可以静态计算权重，因为在大多数情况下参数在推理过程中是固定的。然而，每个输入样本的激活图都不同（等式 1 中的 \(x\)）。因此，有两种量化激活的方法：动态量化 和 静态量化。

在动态量化中，这个范围是在运行时为每个激活图动态计算的。这种方法需要实时计算信号统计数据（最小值、最大值、百分位数等），这可能会产生非常高的开销。然而，动态量化通常会带来更高的精度，因为每个输入的信号范围都是精确计算的。

另一种量化方法是静态量化，其中剪切范围是预先计算的并且在推理过程中是静态的。这种方法不会增加任何计算开销，但与动态量化相比，它通常会导致较低的精度。

动态量化 动态计算每次激活的限幅范围，并且通常可以达到 最高的精度。然而，动态计算信号的范围非常昂贵，因此，从业者最常使用静态量化，其中所有输入的限幅范围都是固定的。

• 微调方法：

高级量化方法：

• 模拟和 Integer-Only 量化

• 混合精度量化

• 硬件感知量化

参考

• 论文：A Survey of Quantization Methods for Efficient Neural Network Inference