困惑度 （Perplexity，PPL） 是评估语言模型的最常见指标之一。在深入研究之前，我们应该注意，该指标专门适用于经典语言模型（有时称为自回归或因果语言模型），并且对于像 BERT 这样的掩码语言模型没有很好的定义。

信息量与信息熵

设随机变量 \(X\) 的概率质量函数为 \(p(X)\)，则 \(X=x\) 这个事件的 信息量 被定义为：

当 \(\log\) 函数的底数等于 \(2\) 时，上式的含义可以被认为是：使用二进制数据对 \(x\) 进行编码所需要的比特数。

比如，当 \(p(x)=1\) 时，不用对消息进行编码我们也知道 \(x\) 一定发生，它对应的信息量等于 \(0\)。而当 \(p(x)=0.5\) 时，\(x\) 发生与不发生的概率各占一般，此时 \(I(x)=1\)，也就是说我们需要 \(1\) 个比特来对 \(x\) 进行编码，可以用 \(0\) 表示不发生，\(1\) 表示发生。

信息熵 则是随机变量的 平均信息量，其定义为：

其中 \(\mathbf{X}\) 是 \(X\) 的样本空间。由于在一个概率分布中，有的事件发生概率大（用尽量少的比特数去编码），有的事件发生概率小，因此使用信息熵可以用来表示编码该分布中一个事件所需的 平均比特数。

概率分布的困惑度

交叉熵

概率模型的困惑度

语言模型

语言模型可以看作是一组概率模型，其中在每个时间点上的概率模型都是对真实世界语言概率分布的建模，具体来说，给定一个 token 序列，语言模型可以给出下一个 token 出现的概率，这里我们用 \(\)p_\xi(X_i\mid X_{<i})\(\) 表示。

另外，利用条件概率公式，通过语言模型也可以计算整个句子的概率：

语言模型的困惑度

语言模型在每个时间点都是对真实世界语言概率分布的建模，因此可以将语言模型看作是真实世界语言随机过程的模型，类似于概率模型的困惑度定义，语言模型的困惑度应该由语言模型本身与真实世界语言随机过程之间的交叉熵来计算，即：

若语言模型同时满足平稳性和遍历性条件，则 \(H(\theta,\xi)\) 又可以写为：

注：关于将渐进均分性质应用到交叉熵的化简我没有找到具体的证明过程，看到的文章基本都是一笔带过，不过结论应该是正确的。

困惑度定义为序列的幂平均负对数似然。如果我们有一个标记化的序列 $X = (x_0, x_1, \dots, x_t)$，那么 \(X\) 的困惑度为：

这也等价于数据和模型预测之间交叉熵（Cross Entropy）的幂。有关困惑度及其与每字符位数 （Bits Per Character，BPC） 和数据压缩的关系的更多直觉，请查看 The Gradient 的精彩博客文章。

自回归语言模型的困惑度计算

计算形式

以上内容我们从原理上讨论了语言模型的困惑度，接下来将考虑如何计算一个自回归语言模型的困惑度。所谓自回归语言模型，指的是使用自回归方法训练的语言模型，具体来说，它使用 token 序列前面的 tokens 来预测下一个 token，然后再与真实的 token 进行比较，从而计算交叉熵损失。这是一种典型的非监督学习方法，目前几乎所有的生成式 LLM 都是使用这种方法进行训练的，所以我们这里只讨论这种类型的语言模型。

根据前面推导的交叉熵计算公式：

这里需要 \(m\) 趋近于无限，但在实际应用中，显然无法处理无限长的序列，所以我们只能使用有限长的数据近似计算，并且 LLM 还存在 context length 限制，于是还需要将评估数据集分割成多个不长于 context length 的子序列，然后分别计算，最后取平均值。也就是说：

其中，\(C\) 为 context lenght，\(N\) 为子序列数量。

如果我们不受模型上下文大小的限制，我们将通过在每一步对整个前一个子序列进行自回归分解和条件来评估模型的困惑度，如下所示。

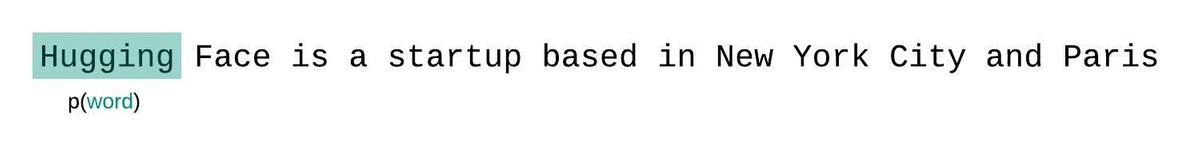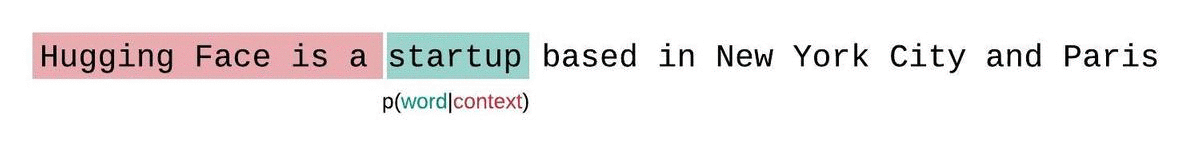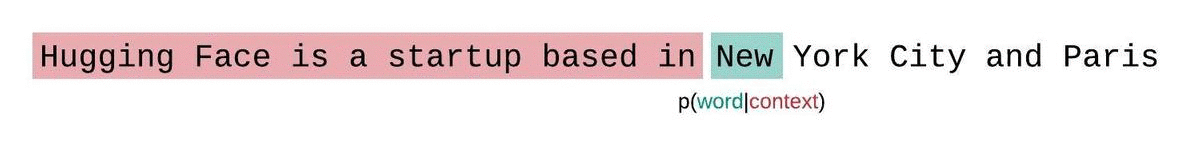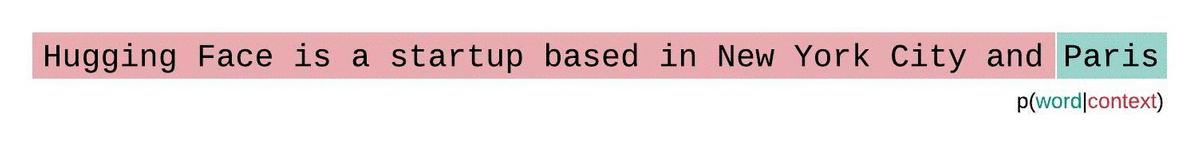
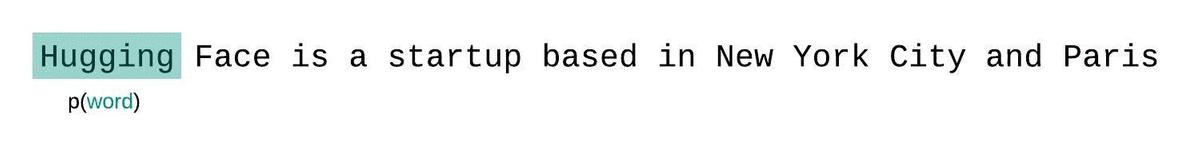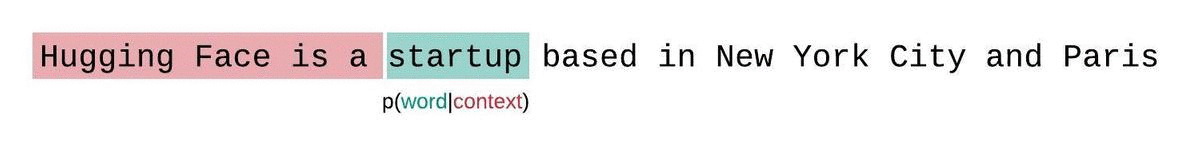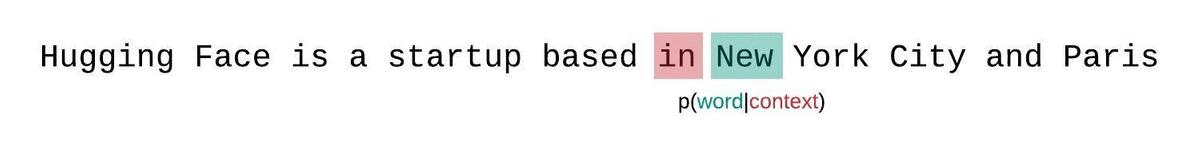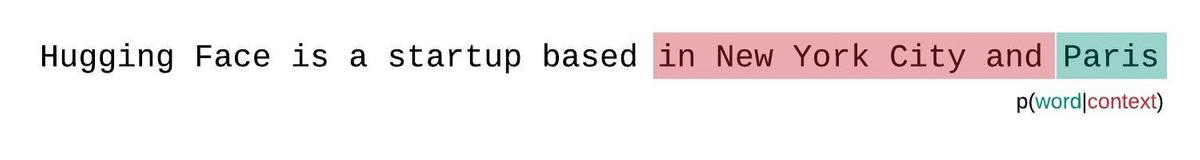
这很容易计算，因为每个段的困惑度都可以在一次前向传递中计算，但作为完全分解困惑度的近似值，并且通常会产生更高（更差）的 PPL，因为模型在大多数预测步骤中具有较少的上下文。

相反，固定长度模型的 PPL 应使用滑动窗口策略进行评估。这涉及反复滑动上下文窗口，以便模型在进行每次预测时具有更多上下文。

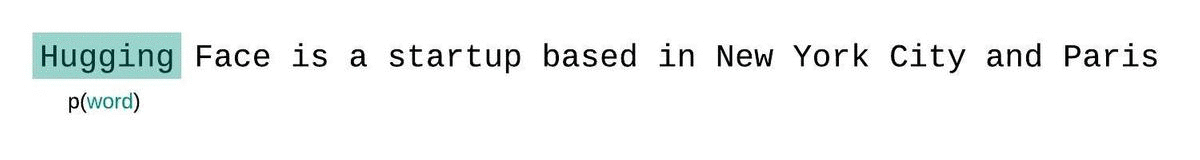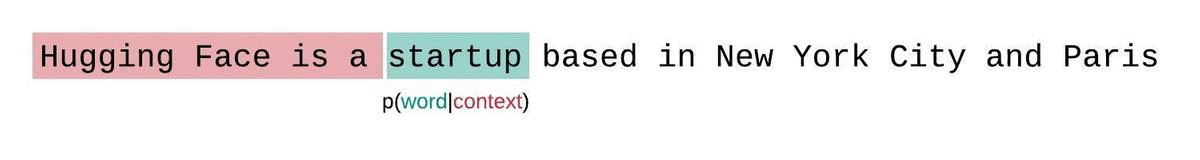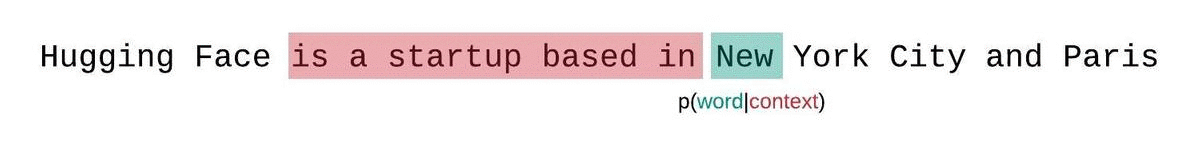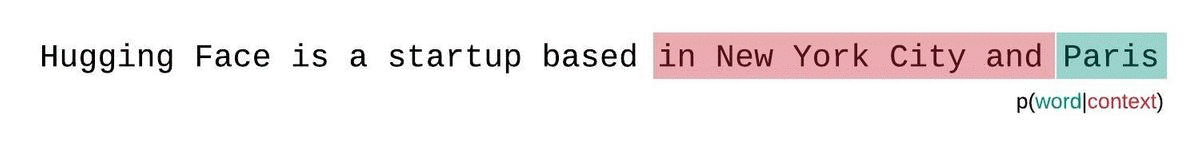
这更接近于序列概率的真实分解，通常会产生更有利的分数。缺点是它需要为语料库中的每个令牌单独转发。一个很好的实际 折衷方案 是采用 跨步滑动窗口，以更大的步幅移动上下文，而不是一次滑动 1 个标记。这使得计算进行得更快，同时仍然为模型提供了一个大的背景，以便在每个步骤中进行预测。

PyTorch 代码

from transformers import GPT2LMHeadModel, GPT2TokenizerFast

device = "cuda"
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)

我们将加载 WikiText-2 数据集，并使用几种不同的滑动窗口策略评估困惑度。由于这个数据集很小，我们只在集合上做一个前向传递，我们可以在内存中加载和编码整个数据集。

from datasets import load_dataset

test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")

import torch
from tqdm import tqdm

max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)

nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
    end_loc = min(begin_loc + max_length, seq_len)
    trg_len = end_loc - prev_end_loc  # may be different from stride on last loop
    input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
    target_ids = input_ids.clone()
    target_ids[:, :-trg_len] = -100

    with torch.no_grad():
        outputs = model(input_ids, labels=target_ids)

        # loss is calculated using CrossEntropyLoss which averages over valid labels
        # N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
        # to the left by 1.
        neg_log_likelihood = outputs.loss

    nlls.append(neg_log_likelihood)

    prev_end_loc = end_loc
    if end_loc == seq_len:
        break

ppl = torch.exp(torch.stack(nlls).mean())
print(ppl)

拆开数据集

虽然把整个数据集当作一个语料，但是这个语料的长度有 394k，显然不能直接送进模型里（截止到 2024 年 3 月，应该还没有上下文窗口达到394k的大语言模型）。（20240611 更新：被 4 月份发布的 kimi 大模型打脸了）

因此需要将数据集拆开，分批次送到模型里。

具体如何拆开？有不同的拆开方式。一个比较粗暴的方式是简单地把数据集做一个切分。比如模型一次性只能处理 4096 个 token，那么把整个语料做如下切分：第 1-4096 个 token 作为第一个数据，第 4097-8192 个 token 作为第二个数据，以此类推。然后依次把每个数据送进模型里，各自计算困惑度。

这种方式比较粗暴，机械地把句子截断，可能会累积产生很多误差。因为在这种方式下，计算的实际上下文比较少。

什么意思呢？比如把第 4097-8192 个 token 作为第二个数据送进去的时候，计算困惑度。

考虑第 4098 个 token，在计算 P(第 4098 个 token | 以往的 context) 的时候，如果按照这种机械截断的方式，这里的 “以往的 context” 只有第 4097 个 token，这样上下文信息太少了。

比较推荐的方式是使用滑窗的方式，也就是 huggingface 官网使用的逻辑。第一次把第 0-4096 个 token 送进去网络，第二次是把第 512-4608 个 token 送进去网络，以此类推……

需要注意一个细节：第一次把第 0-4096 个 token 送进去网络，这是没有问题的。第二次，做了一个长度为 512 的滑窗，把第 512-4608 个 token 送进去网络。请注意，第 512-4096 个 token 在第一次已经被计算过一次生成概率了，这里会再重复计算一次。

为了避免被重复计算，在计算 loss 的时候，需要将第 512-4096 个 token 的 label 置为-100。具体的细节会在后文详细说明。从第二次开始，相当于每次只计算最后 512（等于滑窗长度）个 token 的概率。

通过 loss 计算困惑度

在 PyTorch 中，计算 Cross Entropy 默认使用的底数是自然对数 \(\exp\)，而非计算机中常用的底数 \(2\)。因此，最后需要对 loss 进行 torch.exp() 处理，而非 2 ** loss。

两种综合方式

在我接触到 transformer 计算困惑度代码之前，我认为的思路应该是：第一次推理，将第 0-4096 个 token 送进模型里，然后计算 loss 得到 \(\exp{\text{CE}_1}\)，然后马上计算 loss 得到困惑度 \(\exp{\text{CE}_2}\)，然后以此类推，将所有的困惑度取个平均。即：

transformer 的代码的思路是，第一次推理，将第 0-4096 个 token 送进模型里，然后计算 loss 得到，然后以此类推，得到所有的 CE，取平均，再计算困惑度：

两种方式虽然有细微区别，但是在达成的目标都是一致的：评估模型重构输入句子的能力。

更多

• The Gradient 的精彩博客文章

参考

• HuggingFace 文档：Perplexity of fixed-length models

• 博客：LLM 的困惑度指标定义及其计算

• 知乎：深入理解语言模型的困惑度(perplexity)