MLP:先线性组合,再进行非线性的激活
MLP 的问题:
1、激活函数固定
梯度消失 、 爆炸
反向传播失效
2、线性组合
过于简单
参数量庞大
效率低下 / 能力有限
KAN:先非线性激活,再进行线性组合
相当于把激活函数放在了连接(边)上
数学上叫做 Kolmogorov-Arnold 表示定理。
单层的 KAN 网络其实没什么,更重要的是 KAN 能够进行多层网络。
KAN 写成矩阵形式,不再是 MLP 的线性组合与激活函数的嵌套,而是激活激活再激活。虽然学习起来相比 MLP 更难,但是 KAN 的非线性表征能力大大提升。
训练算法:
MLP 通过增加网络宽度和深度提升性能,需要独立训练不同大小的模型。
KAN 提出了 网格扩展技术,先粗后精,递进精调,无需重训就能实现模型精度的提升。
此外,KAN 还提出了新的网格结构自适应算法。在初始的网络上,通过稀疏化剪枝,设定特定的激活函数,训练仿射参数,符号化等步骤进行优化,大大提升了网络的可解释性。
比如,拟合函数 $f(x, y) = xy$,最终结构长这样。x、y 经过直线求和,
这带来了两大好处:
正着用算法:可以实现数据内在模式的探索和发现
反着用算法L:能把世界模型和学科知识嵌入到网络结构
凡事都有两面性,来看看 KAN 的缺点:
官方代码目前跑起来还比较慢,工程化尚且不足
数学层面,核心的 K-A 表示定理能否扩展到深层网络,还有待论证
B 样条曲线
参考:
在数学中,样条曲线是由多项式分段定义的函数。一般的 Spline 可以是特定区间的 3 阶多项式。在插值问题中,样条插值通常优于多项式插值,因为即使使用低次多项式,也能产生类似的精度结果,同时避免了高次多项式的 Runge’s phenomenon(在一组等距插值点上使用高次多项式进行多项式插值时出现的区间边缘振荡问题)。
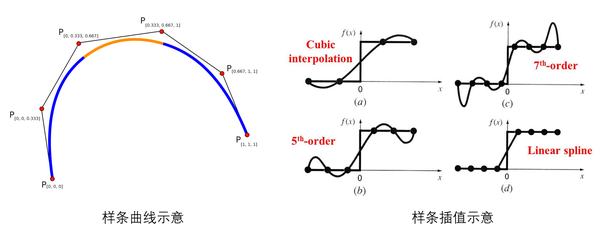
B-spline 算法是整条曲线用一段一段的曲线连接而成,采用分段连续多段式生成。
节点点
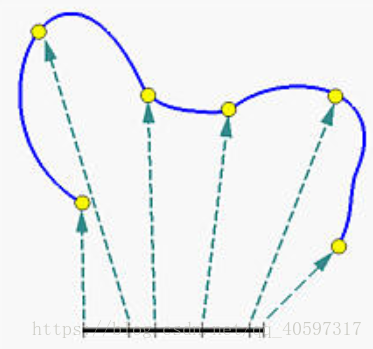
如下图,这里有 5 段曲线组成了整个曲线。下面的直线定义域为 $[0,1]$,就是 $[0,1]$ 被分成五段
可以看出,这里定义域被 节点 细分,节点分别是 $0,\ 0.2,\ 0.4,\ 0.6,\ 0.8,\ 1$,6 个节点正好可以把定义域(即下面的黑色线段)分成 5 段。
6 个节点分别对应于曲线上的一个点,可以用 $C(u_i)$ 代表对应的曲线上的点,$C(u_i)$ 被称为 节点点(knot point),节点点把 B-样条曲线划分成 5 个曲线段,每个都定义在一个节点区间上。这些曲线段都是 $k$ 阶的贝塞尔曲线。
节点(knots)
如果有 $u_0 \leq u_1 \leq u_2 \leq … u_{m-1} \leq u_m$,那么称 $u_i$ 为节点,显然,上述图片的 $m = 5$。
设 $U$ 是 $m+1$ 个非递减数的集合,那么有 ${u_0, u_1, …, u_m}$,集合 $U$ 称为 节点向量(knot vector)。
如果 $u_i = u_{i+1} = … = u_{i+k+1}$,那么 $u_i$ 是一个重复度(multiplicity) 为 $k$ 的多重节点,$k>1$。否则,如果一个节点只出现一次,那么这就是一个简单节点。如果节点等间距,节点向量或节点序列称为均匀的;否则它是非均匀的。
$[u_i, u_{i+1})$ 是第 $i$ 节点的区间,$i=0,1,…,m$。
所有的 B 样条基函数都被假设在定义域 $[u_0, u_m]$ 上,通常 $u_0=0$,$u_m = 1$。
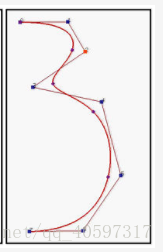
如下图所示,这里有 8 个控制点,依次用线段连接(组成多边形),B样条曲线由一系列 5 条 2 阶的贝塞尔曲线连接形成。
一般阶数越低(即 p 越小),那么 B 样条曲线就更容易逼近他它的控制折线。
一般表达
有 $n+1$ 个控制点 $P_i\ (i=0,1,…,n)$ 和一个节点向量 $U={u_0, u_1, …, u_m}$,依次连接这些 控制点 可以构成一个 特征多边形,k 阶($k - 1$ 次)B 样条曲线的表达式为($2<=k<=n+1$),必须满足 m = n + k + 1 \(p(U) = \sum_{i=0}^n P_i N_{i, k}(u)\) 其中,
$N_{i, k}(u)$ 是 k 阶 B 样条基函数,也叫调和函数,或者 k阶规范 B 样条基函数;
$N_{i, k}(u)$ 是第 $i$ 个 $k$ 阶 B 样条基函数,$i=0,1,…, m$
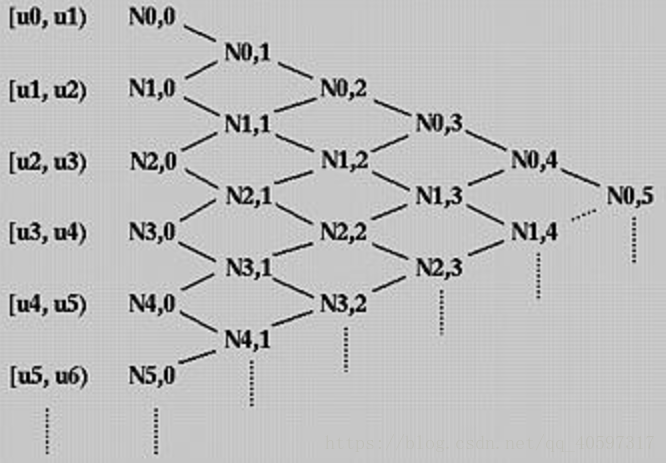
下面为 $N_{i, k}(u)$ 的 Cox-de Boor 递推公式:
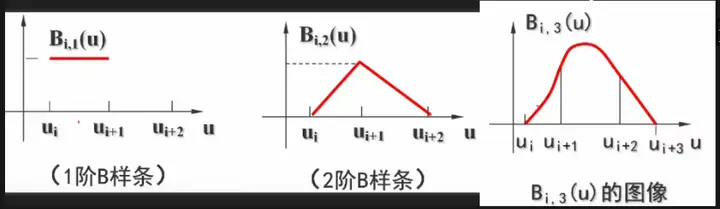
上图是基函数的运算关系,从左向右,从上往下可以依次计算各个基函数。
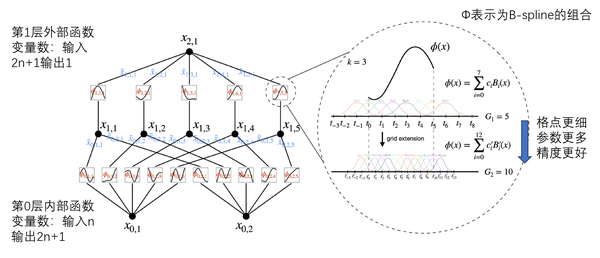
可学习的激活函数
可学习的激活函数 \(\phi(x)\):\(\phi(x) = w(b(x) + \text{spline}(x))\)
basic function \(b(x)\) 和 spline function \(\text{spline}(x)\)
basic function 设置为 \(b(x) = \text{silu}(x)=\frac{x}{1+e^{-x}}\)
spline function 被参数化为:一系列 B-Spline 的线性组合
- \[\text{spline}(x) = \sum_i c_i B_i(x)\]
- \(c_i\) 是可学习的参数
实际上,在官方代码的实现中,将 \(\phi(x)\) 公式化为: \(\phi(x) = \text{scale\_base} * b(x) + \text{scale\_spline} * \text{spline}(x)\) 其中,scale_base 初始化为 \(\frac{1}{\sqrt(d_{in} + e)}\),\(e\) 为 grid_eps,是一个很小的数,防止分母为零。
scale_base 和 scale_spline 均为可训练的参数。

Efficient-KAN 代码
参考
论文:
bilibili:
文档信息
- 本文作者:Bookstall
- 本文链接:https://bookstall.github.io/2024/05/19/kan-learn/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)