State Space Model

前言

Transformer

RNN

State Space Model（SSM）

状态空间

状态空间模型

RNN 本质上也是一个状态空间模型

SSM 是用于描述这些状态表示并根据某些输入预测其下一个状态可能是什么的模型。

SSM 的两个方程：状态方程与输出方程

SSM 的关键是找到：状态表示 \(h(t)\)，以便结合输入序列 \(x(t)\) 来预测输出序列 \(y(t)\)。

而这两个方程也正是状态空间模型的核心。

此时，在 SSM 中，即便是在不同的输入之下，矩阵 \(A\)、\(B\)、\(C\)、\(D\) 都还是 固定不变 的，但到了后续的改进版本 Mamba 中则这 4 个矩阵都是随着输入不同而可变的参数。

\[h^\prime(t) = Ah(t) + Bx(t)\] \[y(t) = Ch(t) + Dx(t)\]

统一视角

最终，我们可以通过下图来统一这两个方程：

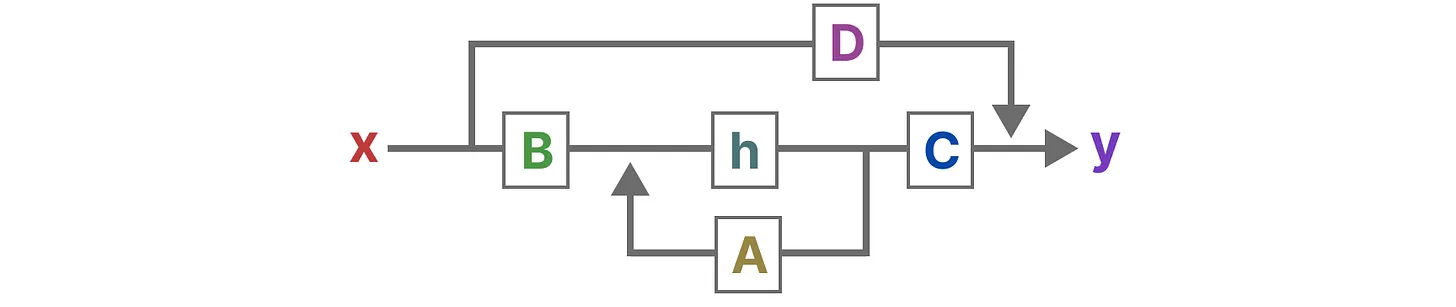
SSM 两个方程的统一

为了进一步加深对该图的理解，对该图进行一步一步地拆解：

1、假设我们有一些输入（的连续）信号 \(x(t)\)，该信号首先乘以矩阵 \(B\)，如下所示：

2、根据上一步的结果，再加上：上一个状态 \(h(t)\) 与矩阵 \(A\) 相乘，从而更新下一个状态：

3、然后，使用矩阵 \(C\) 将当前状态和输入信号转换为输出：

4、最后，再利用矩阵 \(D\) 提供直接从输入 \(x(t)\) 到输出的直接信号（通常也被称为 Skip Connection）：

5、此外，如果没有矩阵 \(D\) 所在的 Skip Connection，那么 SSM 通常被视为：

综上所述，SSM 的核心结构如下图所示：

SSM 的两个核心方程可以根据观测数据预测系统的状态，并且考虑的输入序列一般都是连续的。因此，SSM 的主要表示是连续时间表示（ continuous-time representation），如下图所示。

从 SSM 到 S4

从 SSM 到 S4 的三步升级：

离散化 SSM
循环、卷积表示
基于 HiPPO 矩阵处理长序列

离散化 SSM：基于零阶保持技术

S4 模型使用四个连续参数 \((\Delta, A, B, C)\) 定义序列到序列的转换过程，分为两个阶段：
阶段一（离散化）：将连续参数 \((\Delta, A, B)\) 转换为离散参数 \((\bar{A}, \bar{B})\)
阶段二：通过离散化后的参数计算序列转换，可以通过线性递归或全局卷积两种方式实现
——参考：Mamba 详解

S4 模型的离散化过程：将四个连续参数 \((\Delta, A, B, C)\) 转化为三个离散参数 \((\bar{A}, \bar{B}, C)\)

由于除了连续的输入之外，还会通常碰到离散的输入(如文本序列)，不过，就算 SSM 在离散数据上训练，它仍能学习到底层蕴含的连续信息，因为在 SSM 眼里，序列不过是连续信号的采样，或者说连续的信号模型是离散的序列模型的概括。

那模型如何处理离散化数据呢？答案是可以利用零阶保持技术（Zero-order hold technique，ZOH）

1、首先，每次收到离散信号时，我们都会保留其值，直到收到新的离散信号，如此操作导致的结果就是创建了 SSM 可以使用的连续信号

2、保持该值的时间由 一个新的可学习参数 表示，称为步长（step）\(\delta\)，表示输入的阶段性保持（resolution）

3、经过上述操作，可以得到连续的输入信号。于时，我们可以生成连续的输出，并且仅根据输入的时间步长对值进行采样。

这些采样值就是 SSM 的离散输出，并且可以针对 \(A、B\) 按如下的方式进行零阶保持，得到新的矩阵：

\[\bar{A} = e^{\Delta A}\] \[\bar{B} = (\Delta A)^{-1} (e^{\Delta B} - I)\cdot \Delta B\]

其中，\(\bar{A}、\bar{B}\) 分别表示离散化之后的新矩阵。

最终，我们能够将连续的 SSM 转换为离散的 SSM。因此，不再是从函数 \(x(t)\) 到函数 \(y(t)\)，而是从序列 \(x_k\) 到序列 \(y_k\)。

这里的矩阵 \(\bar{A}、\bar{B}\) 表示的就是离散 SSM 模型的参数，并且这里的序列使用下标 \(k\)，而不再是使用 \(t\) 来表示离散的时间步长。

注意：我们在保存时，仍然保存矩阵 \(A\) 的连续形式（而非离散化版本）。只是在训练过程中，连续表示被离散化（During training, the continuous representation is discretized）。

循环结构表示：方便快速推理

能够实现与 RNN 类似的 线性推理（\(O(n)\)）

离散 SSM 允许可以用离散时间步长重新表述问题，在每个时间步，都会涉及到隐藏状态 \(h_k\) 的更新。例如，\(h_k\) 取决于 \(\bar{B}x_k\) 和 \(\bar{A}h_{k-1}\) 的共同作用结果，然后再通过 \(Ch_k\) 预测输出结果 \(y_k\)。

具体过程如下图所示：

此时，SSM 模型与 RNN 的结构非常相似。我们可以使用与 RNN 相似的结构来进行 快速推理。如下图所示：

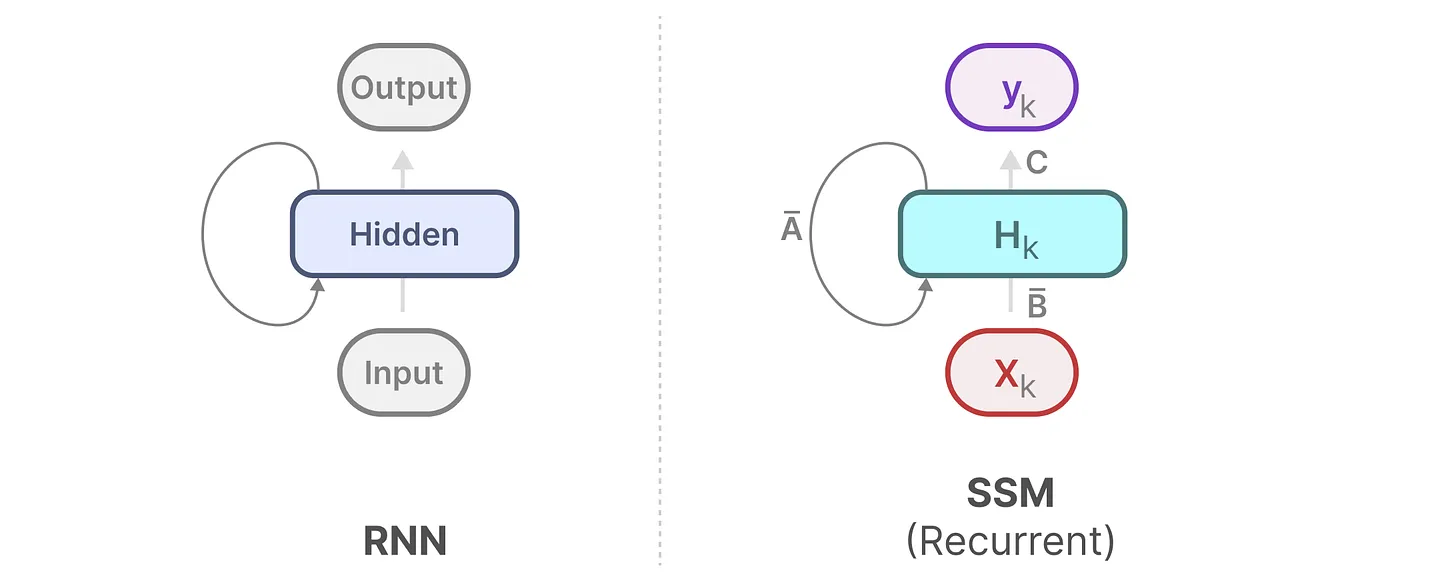
RNN 与 SSM 模型的比较

对 SSM 模型进行展开，\(h_k\) 始终是由 \(\bar{A}h_{k-1}\) 和 \(\bar{B}x_t\) 共同更新的，如下图所示：

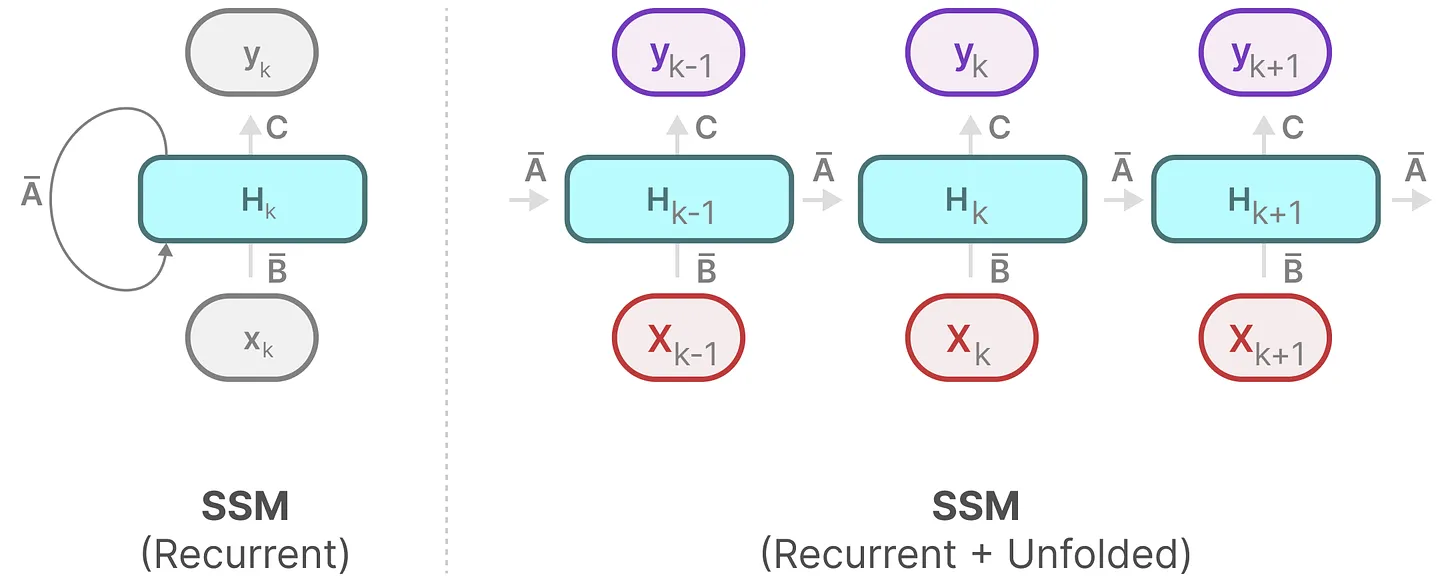
SSM 展开之后的结构图

卷积结构表示：方便并行训练

然而，与 RNN 模型相似，在对 SSM 模型进行训练时，也会遇到 无法并行（（parallelized））训练 的问题。

我们首先对输出方程 \(y_k = Ch_k\) 进行展开：

\[\begin{aligned} y_0 &= Ch_0 \\ &= C\bar{A}^0\bar{B}x_0 \end{aligned} \begin{aligned} y_1 &= Ch_1 \\ &= C(\bar{A}h_0+\bar{B}x_1) \\ &= C\bar{A}^1\bar{B}x_0 + C\bar{A}^0\bar{B}x_0 \end{aligned} \begin{aligned} y_2 &= Ch_2 \\ &= C\bar{A}^2\bar{B}x_0 + C\bar{A}^1\bar{B}x_0 + C\bar{A}^0\bar{B}x_0 \end{aligned} \begin{aligned} y_3 &= Ch_3 \\ &= C\bar{A}^3\bar{B}x_0 + C\bar{A}^2\bar{B}x_0 + C\bar{A}^1\bar{B}x_0 + C\bar{A}^0\bar{B}x_0 \end{aligned}\]

我们将 \(y_2\) 的结果换一种表示方法，如下所示：

\[y_2 = \begin{pmatrix} C\bar{A}^0\bar{B} & C\bar{A}^1\bar{B} & C\bar{A}^2\bar{B} \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \end{pmatrix}\]

其中，右侧向量就是我们的输入 \(x\)。

由于三个离散参数 \(\bar{A}、\bar{B}、C\) 都是常数，我们可以预先计算左侧向量，并将其保存为一个卷积核 \(\bar{K}\)。

这为我们提供了一种使用 卷积核 \(\bar{K}\) 实现高效计算 \(y_k\) 的简单方法，如下所示：

\[\bar{K} = \begin{pmatrix} C\bar{A}^0\bar{B} & C\bar{A}^1\bar{B} & C\bar{A}^2\bar{B} \end{pmatrix}\] \[y = \bar{K} * x\]

上面的公式还可以参考下图：

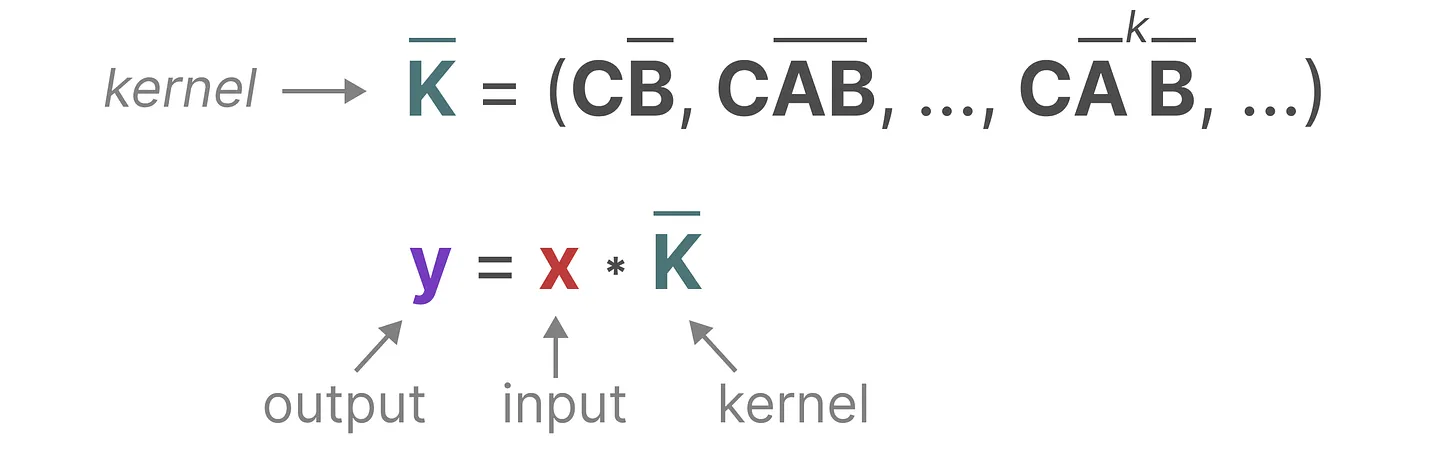
SSM 模型卷积表示的示意图

还需要特别注意的是，对于不同步长的输入 \(x_k\)，使用不同大小的卷积核来处理。例如：

处理 \(y_0\)，理论上需要大小为 1 的卷积核
处理 \(y_1\)，理论上需要大小为 2 的卷积核
处理 \(y_2\)，理论上需要大小为 3 的卷积核

小结

至此，我们可以将 SSM 表示为卷积的一个主要好处是它可以像卷积神经网络 CNN 一样进行并行训练。然而，由于内核大小固定，它们的推理不如 RNN 那样快速。

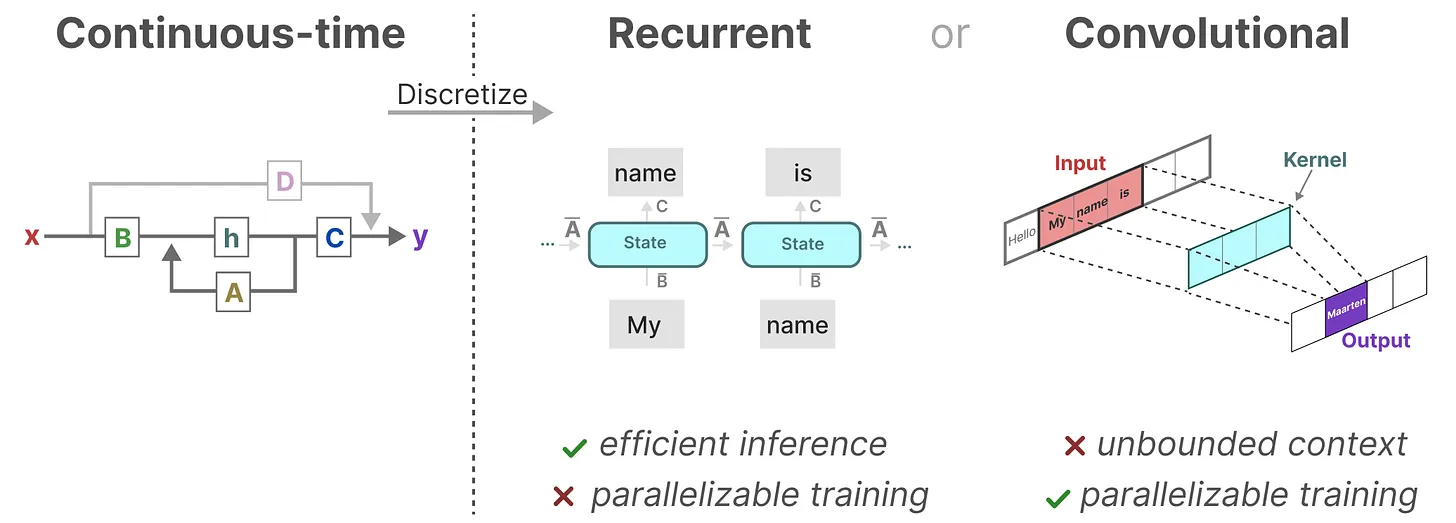
SSM 模型的循环表示与卷积表示示意图

那么，有没两全其美的办法呢？答案是有的。

作为从输入信号到输出信号的参数化映射，SSM 模型可以看做是 RNN 与 CNN 的结合：

训练阶段：使用 CNN 表示
推理阶段：使用 RNN 表示

SSM 模型在训练阶段使用卷积表示，在推理阶段使用循环表示

可视化说明

在经典的图像识别任务中，我们用过滤器（即卷积核 kernels）来导出聚合特征，如下所示：

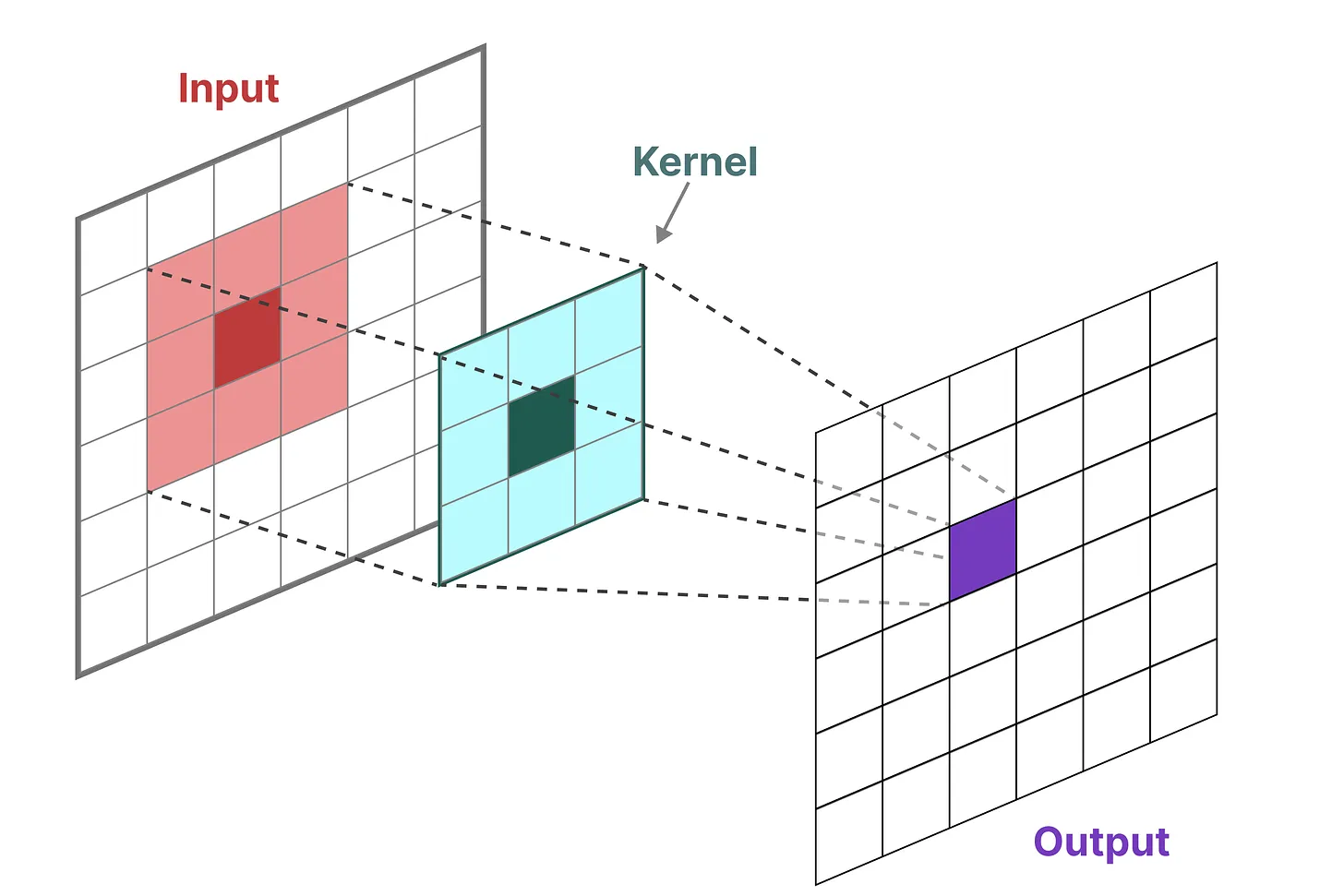
处理二维图像的卷积核示意图

由于我们处理的是文本而不是图像，因此我们需要一维视角：

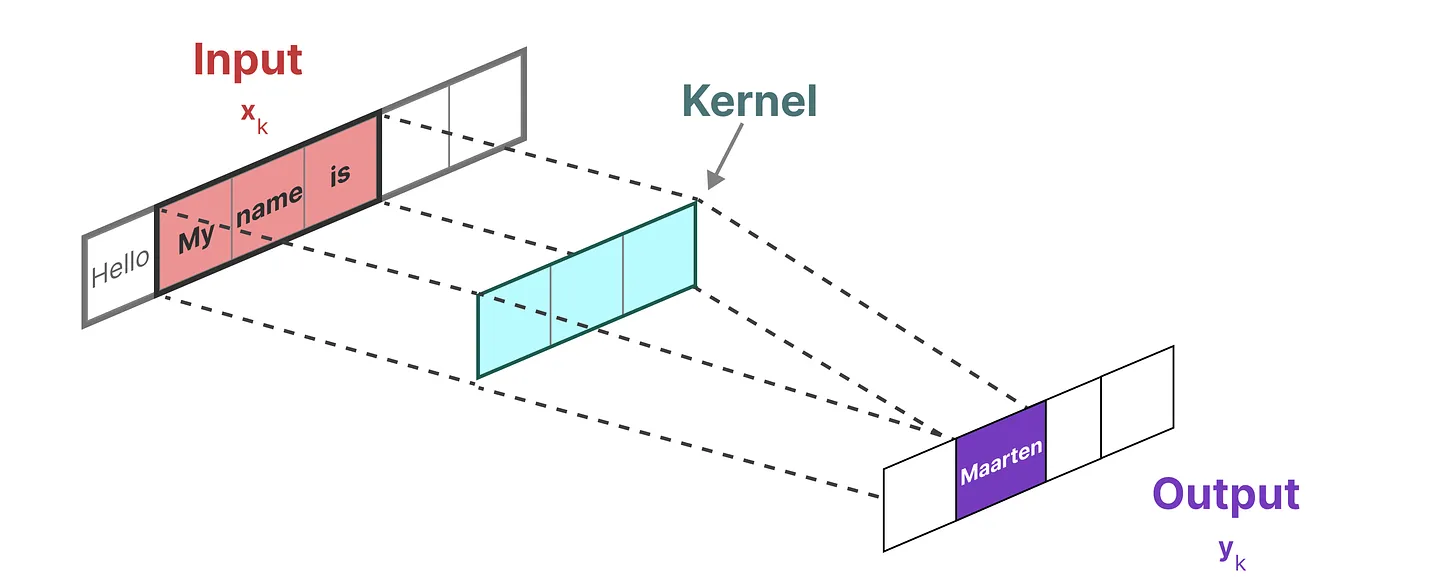
处理文本数据的卷积核示意图

本文咱们还是通过一个例子一步一步进行理解。

1、与卷积一样，我们可以使用 SSM 内核来检查每组 token 并计算输出：

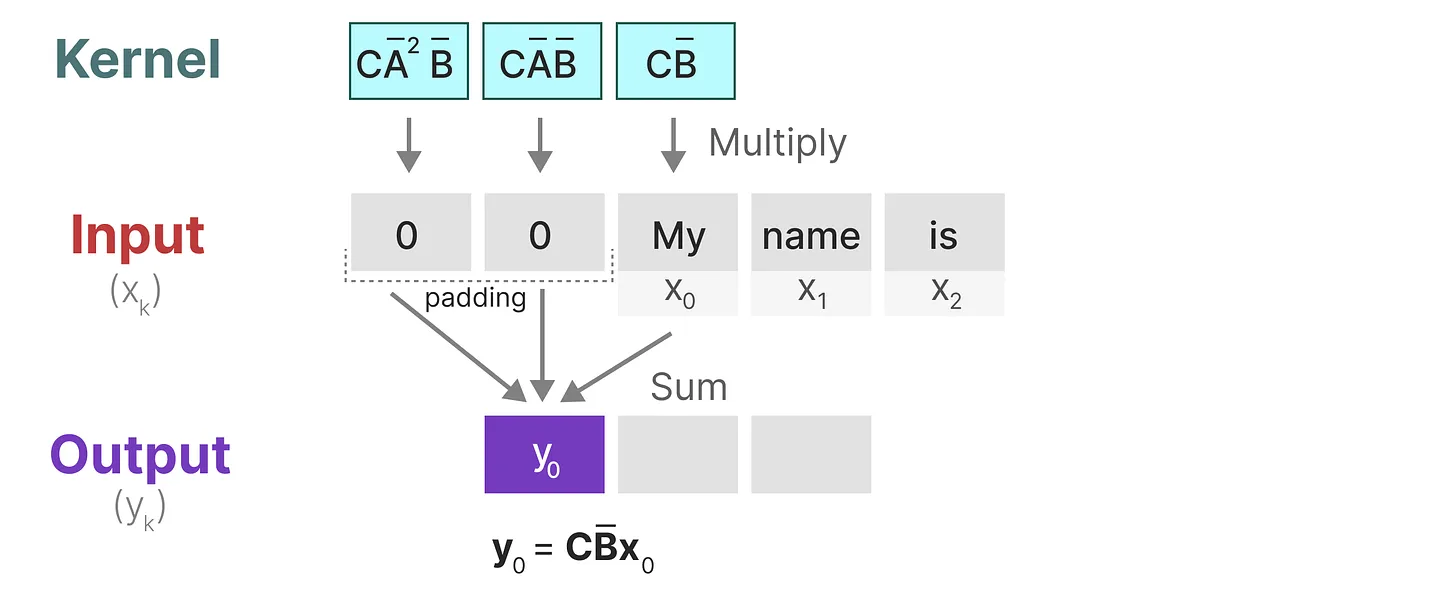
2、移动一次卷积核，并执行下一步的计算：

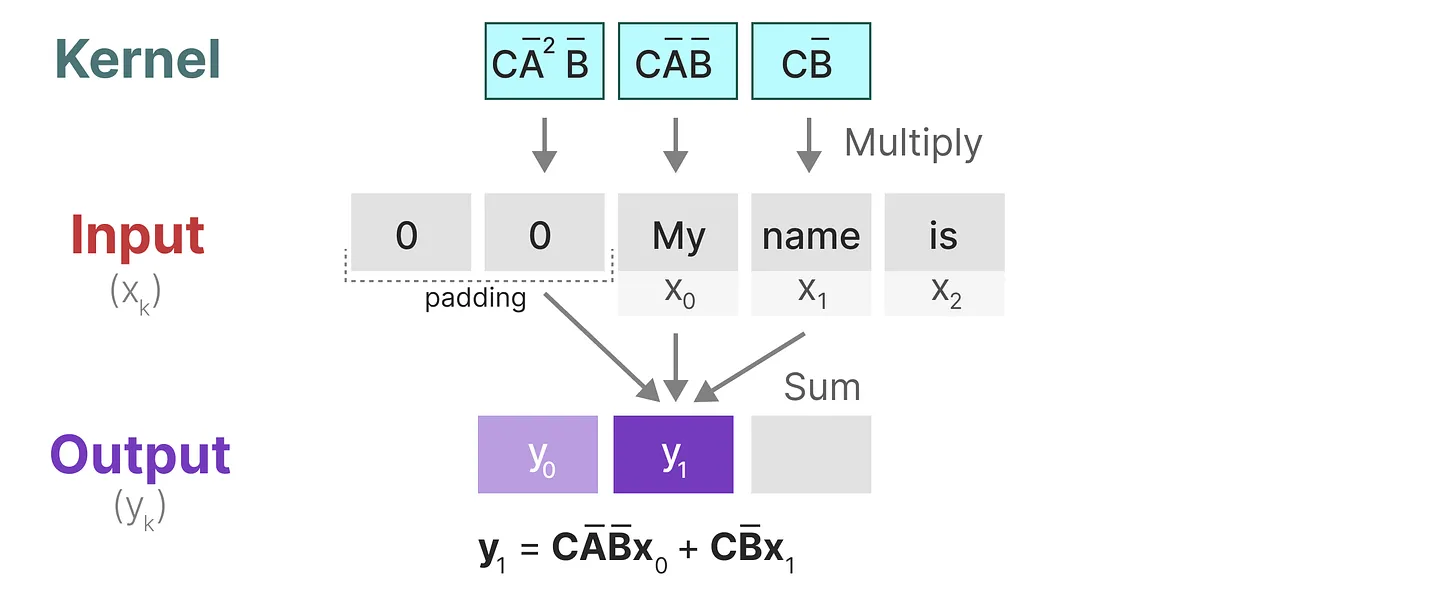
3、移动一次卷积核，并执行下一步的计算：

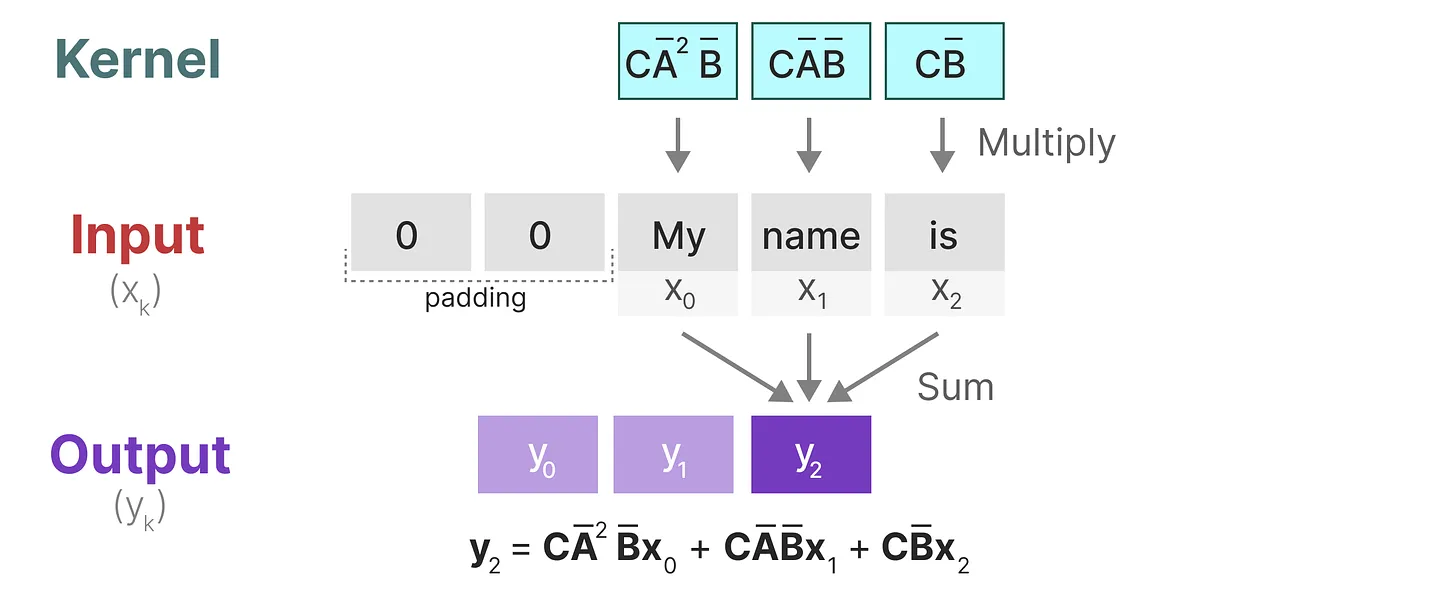
HiPPO 矩阵：处理长程依赖问题

与 RNN 类似，SSM 在建模较长序列时也会遇到梯度消失/爆炸问题。

为了解决这个问题，HiPPO（High-order Polynomial Projection Operator）模型结合了递归内存和最优多项式投影的概念，可以显着提高递归内存的性能，这种机制对于 SSM 处理长序列和长期依赖关系非常有帮助。

如我们之前在循环表示中看到的那样，矩阵 \(\bar{A}\) 捕获先前状态的信息来构建新状态。当 \(k = 5\) 时，有 \(h_5 = \bar{A}h_4+\bar{B}x_5\)，如下图所示：

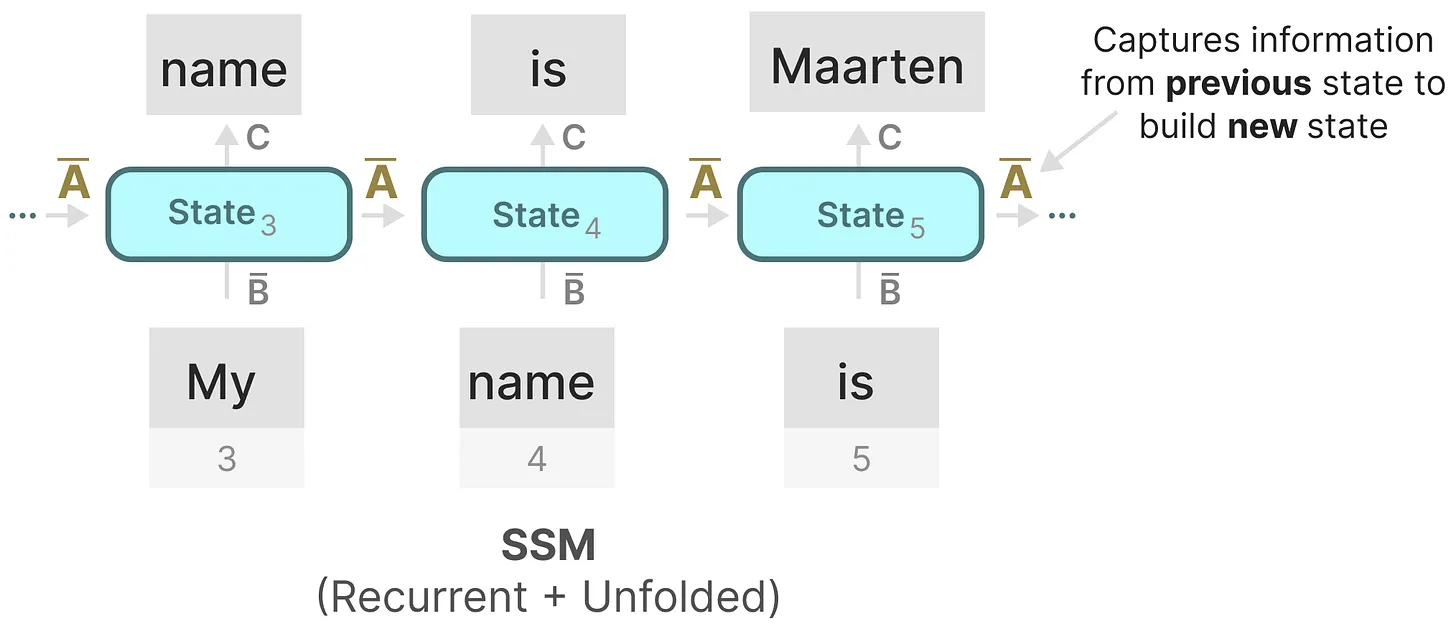
在这个意义上，我们可以认为矩阵 \(\bar{A}\) 产生了隐藏状态，如下图所示：

HiPPO 尝试将当前看到的所有输入信号压缩为系数向量，并使用 HiPPO 矩阵 \(A\) 构建一个 “可以很好地捕获最近的 token 并衰减旧的 token ” 的状态表示，如下图所示：

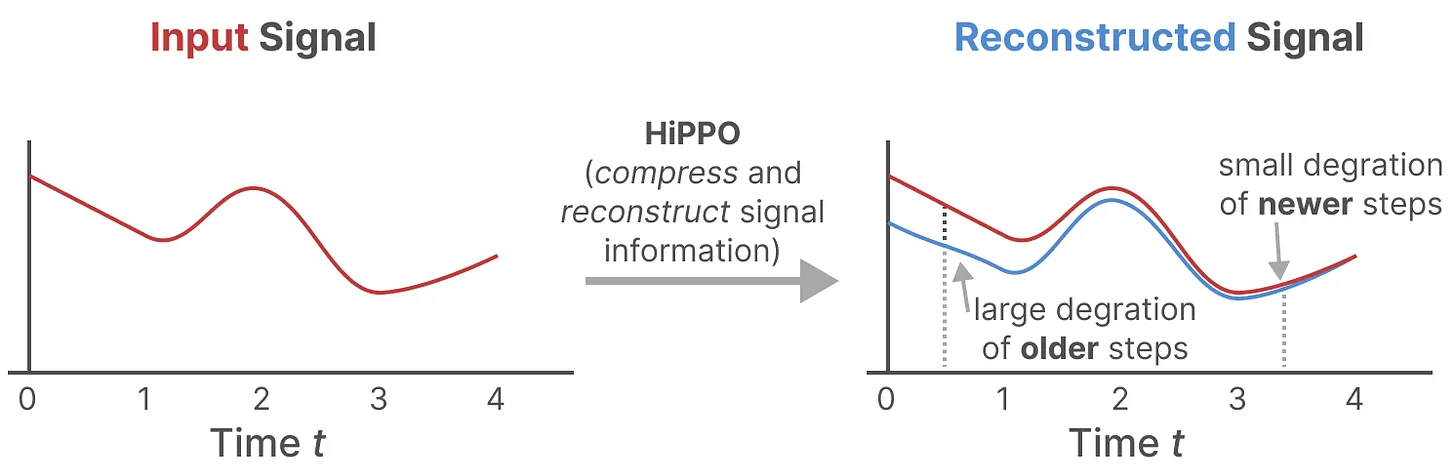
也就是说，通过函数逼近产生状态矩阵 A 的最优解，其公式可以表示如下：

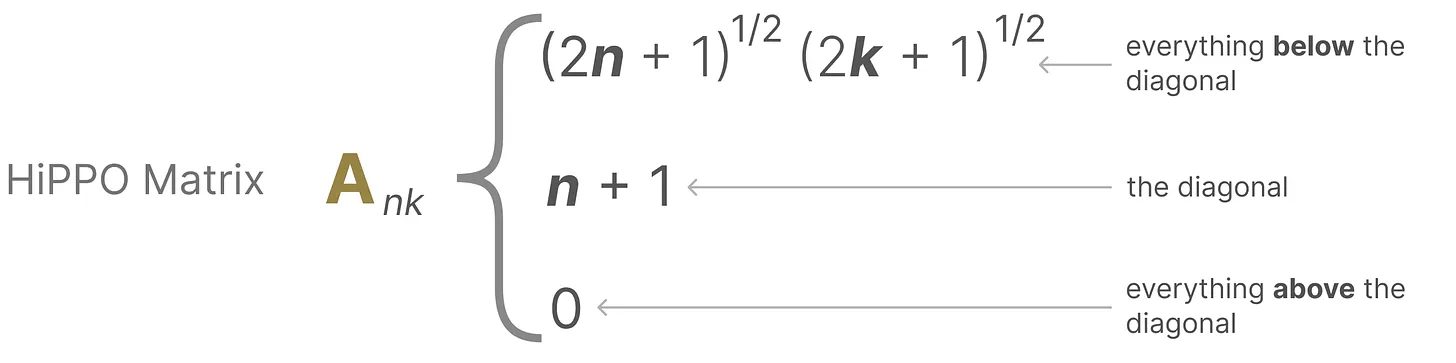
HiPPO 矩阵的公式表示

HiPPO 矩阵的示意图如下所示：

HiPPO 矩阵的示意图

正由于 HiPPO 矩阵可以产生一个隐藏状态来记住其历史（从数学上讲，它是通过跟踪 Legendre polynomial 的系数来实现的，这使得它能够逼近所有以前的历史），使得在被应用于循环表示和卷积表示中时，可以处理远程依赖性。

至此，我们就可以得到 S4（Structured State Space for Sequences，序列的结构化状态空间）模型，该模型是一个能够处理长序列的 SSM 模型，如下图所示：

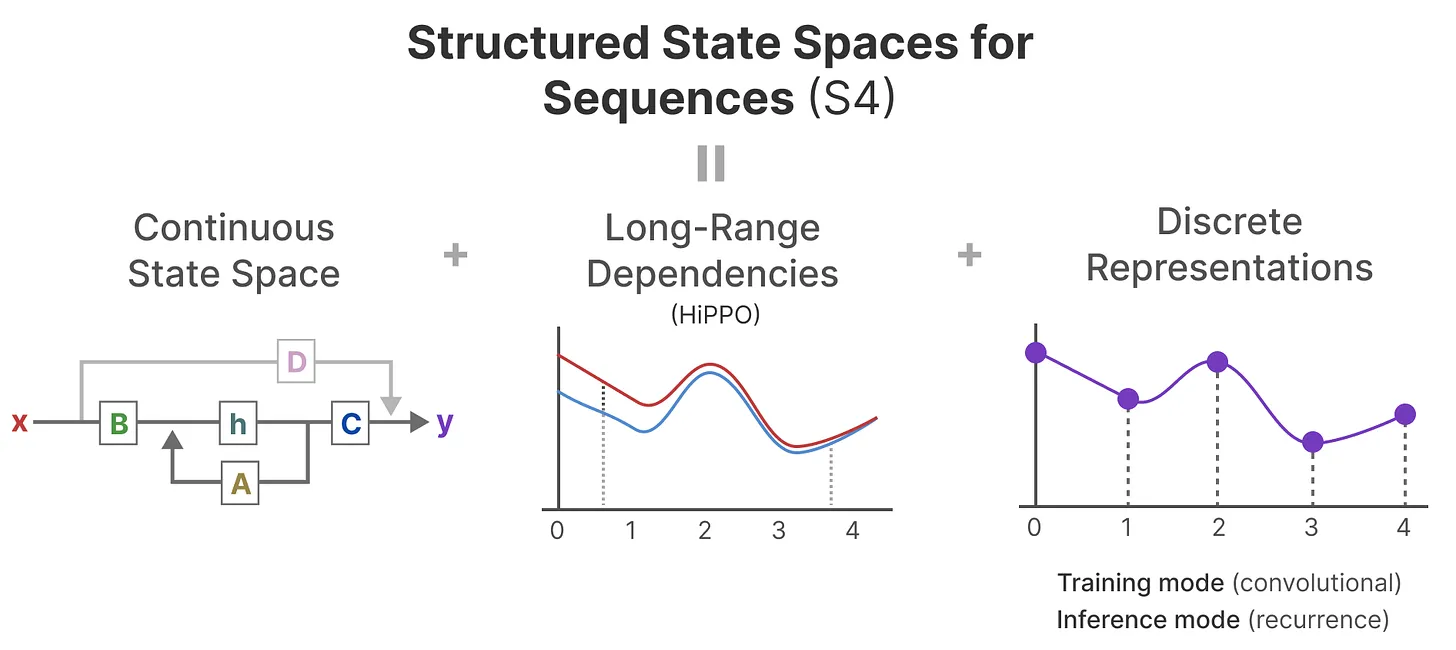
S4 模型的示意图

并且，S4 对 HiPPO 矩阵 \(A\) 进行了对角化，如下图所示：

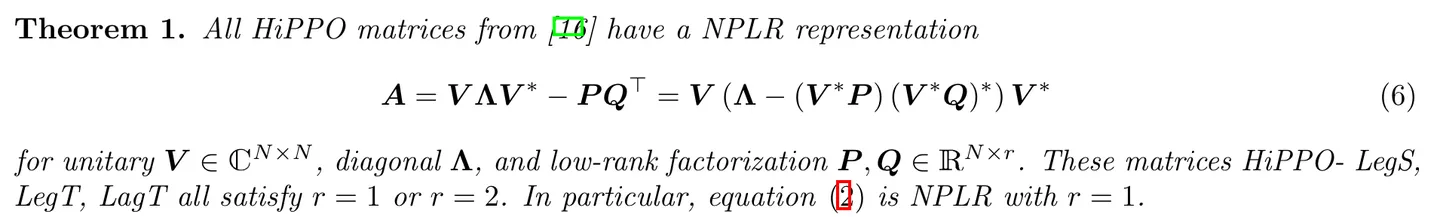
HiPPO 矩阵的对角化

SSM & S4 的问题：

线性时间不变性（LTI）

这里的不变性特指 不随输入变化而变化。但是，在输入确定之后，在 训练过程 中，这些矩阵是可以根据需要去做 梯度下降而变化的

线性时间不变性（Linear Time Invariance，LTI）规定了 SSM 模型中的 \(\bar{A}、\bar{B}、C\) 不随输入不同而不同。这意味着：

对于 SSM 生成的每个 token，矩阵 \(\bar{A}、\bar{B}、C\) 都是相同的
SSM 无法针对输入做针对性的推理

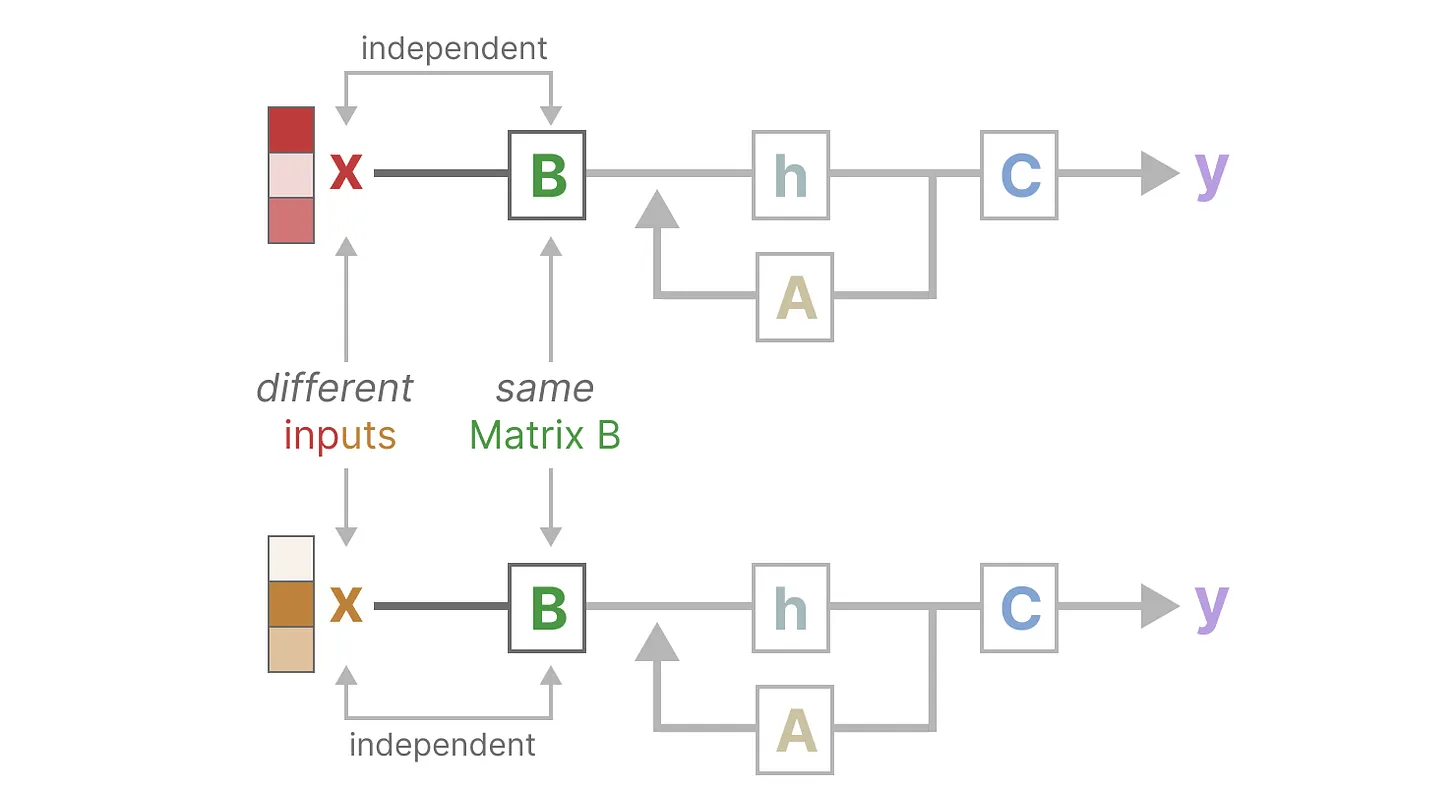
LTI 的示意图

同样，无论输入如何，\(\bar{A}\) 和 \(C\) 也保持固定，如下图所示：

S4 缺乏选择性：一视同仁

如何改进 S4 以根据各个 token 重要性程度的不同而选择性聚焦？

下面一个简单的示例。

对于 “I want to order a hamburger.” 这个句子：

如果没有选择性，则 S4 会花费相同的 “精力” 来处理每个单词：

如果是一个试图对这句话的意图进行分类的模型，它可能会想更多地 “关注” order、hamburger，而不是 want、to：

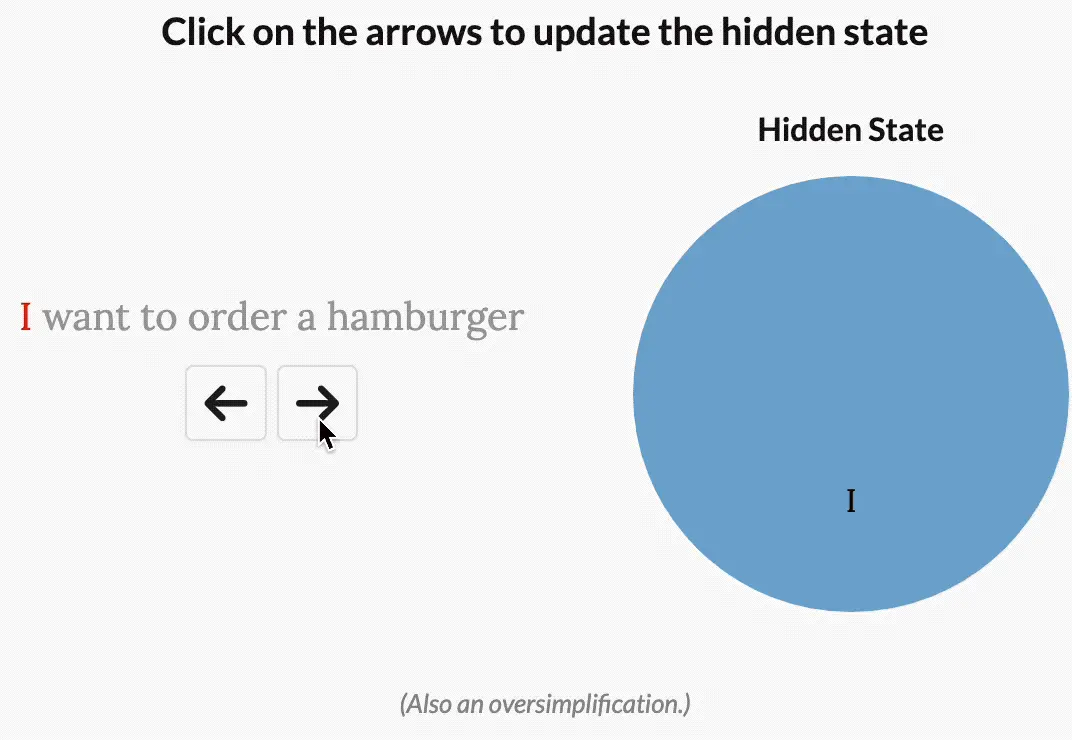
解决方法：Mamba

虽然 Mamba 可以 “专注于” 输入中对于当前任务更重要的部分，但坏处是没法再通过 CNN 做并行训练了，原因在于：

在 S4 中，我们可以预先计算该内核、保存，并将其与输入 \(x\) 相乘，因为离散参数 \(\bar{A}、\bar{B}、C\) 是恒定的
然而，在 Mamba 中，这些矩阵会根据输入而变化！因此，我们无法预先计算卷积核 \(\bar{K}\)，从而无法使用 CNN 的计算模式来并行训练 SSM 模型

在 Mamba 中，卷积核的计算方式不再适用

如果我们想要选择性，得用 RNN 模式进行训练。然而，RNN 的训练速度非常慢，所以我们需要找到 一种无需卷积的并行训练方式。

Mamba（S6）

与先前的研究相比，Mamba 主要有三点创新：

1、对输入信息有选择性处理（Selection Mechanism）

S4 与 S6 的算法流程

2、硬件感知的算法（Hardware-aware Algorithm）

该算法采用 “并行扫描算法” 而非 “卷积” 来进行模型的循环计算（使得不用 CNN 也能并行训练），但为了减少 GPU 内存层次结构中不同级别之间的 IO 访问，它没有具体化扩展状态

当然，这点也是受到了 S5 的启发

3、更简单的架构

将 SSM 架构的设计与 transformer 的 MLP 块合并为一个块，来简化过去的深度序列模型架构，从而得到一个包含 selective state space 的架构设计

选择性扫描

作者认为，序列建模的一个基础问题是把上下文压缩成更小的状态(We argue that a fundamental problem of sequence modeling is compressing context into a smaller state)，从这个角度来看

transformer 的注意力机制虽然有效果但效率不算很高，毕竟其需要显式地存储整个上下文（KV 缓存），直接导致训练和推理消耗算力大好比，Transformer 就像人类每写一个字之前，都把前面的所有字+输入都复习一遍，所以写的慢。

RNN 的推理和训练效率高，但性能容易受到对上下文压缩程度的限制。

好比，RNN 每次只参考前面固定的字数，写的快是快，但容易忘掉更前面的内容。

而 SSM 的问题在于其中的矩阵 A B C 不随输入不同而不同，即无法针对不同的输入针对性的推理。

SSM 的线性时间不变性

Mamba 的解决办法是，相比 SSM 压缩所有历史记录，Mamba 设计了一个简单的选择机制，通过 “参数化 SSM 的输入”，让模型对信息有选择性处理，以便关注或忽略特定的输入

这样一来，模型能够过滤掉与问题无关的信息，并且可以长期记住与问题相关的信息

好比，Mamba 每次参考前面所有内容的一个概括，越往后写对前面内容概括得越狠，丢掉细节、保留大意

为方便大家对比，通过如下表格总结下各个模型的核心特点：

模型	对信息的压缩程度	训练的效率	推理的效率
Transformer	Transformer 对每个历史记录都不压缩	训练消耗算力大	推理消耗算力大
RNN	随着时间的推移，RNN 往往会忘记某一部分信息	RNN 没法并行训练	推理时只看一个时间步，故推理高效（推理快、但训练慢）
CNN		训练效率高，可并行
SSM	SSM 压缩每一个历史记录	通过构造卷积核，实现并行	矩阵不因输入不同而不同，无法针对输入做针对性推理
Mamba	选择性的关注必须关注的、过滤掉可以忽略的	Mamba 每次参考前面所有内容的一个概括，兼备训练、推理的效率	类似 RNN 的推理过程，可实现针对性推理

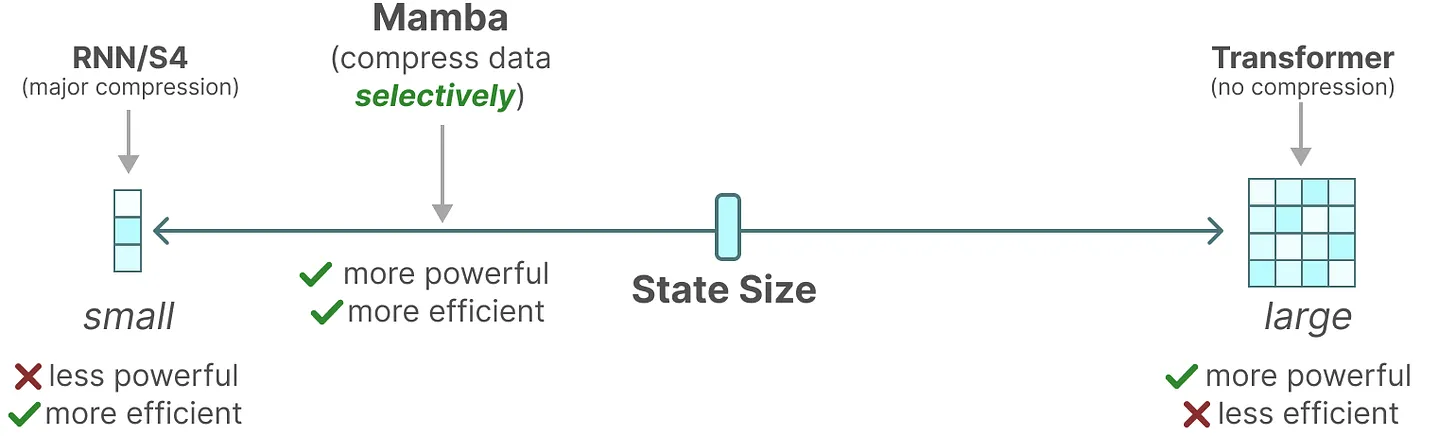
总之，序列模型的效率与效果的权衡点在于它们对状态的压缩程度：

高效的模型必须有一个小的状态（比如 RNN 或 S4）
而有效的模型必须有一个包含来自上下文的所有必要信息的状态（比如transformer）

硬件感知

并行计算（前缀和）

对于 S4 模型而言，由于 卷积核 的参数是随输入数据 动态变化 的，因此，我们无法通过预先计算卷积核来实现并行计算。

我们只能在 RNN 模式下对 S4 模型进行训练，这又改如何实现并行计算呢？

首先，我们重新分析 S4 模型的两个方程，可以发现：

输出结果 \(y_3\) 与输入数据 \(x_3、x_2、x_1、x_0\) 有关

S4 模型输入结果的示意图

这与前缀和问题非常相似

前缀和的示意图

对于前缀和，我们可以将其公式化为：

\[h_k = h_{k-1} + x_k\]

而对于 Mamba 的隐藏状态更新公式：

可以看出，上述两个公式 非常相似。也就是说，我们可以借鉴前缀和的并行算法来实现 Mamba 模型的并行训练。

并行前缀和算法的示意图如下所示：

并行计算前缀和的示意图

图片来源：https://commons.wikimedia.org/w/index.php?curid=14985743

其中，每条竖线代表数组中的一个元素。具体说明，也可以参考数组的前缀和（Prefix Sum）问题及其并行算法。

每个状态比如 \(h_1\) 都是前一个状态比如 \(h_0\) 乘以 \(\bar{A}\)，加上当前输入 \(x_1\) 乘以 \(\bar{B}\) 的总和，这就叫 扫描操作（scan operation），可以使用 for 循环轻松计算，然这种状态之下想并行化是不可能的（因为只有在获取到前一个状态的情况下才能计算当前的每个状态）。如下图所示：

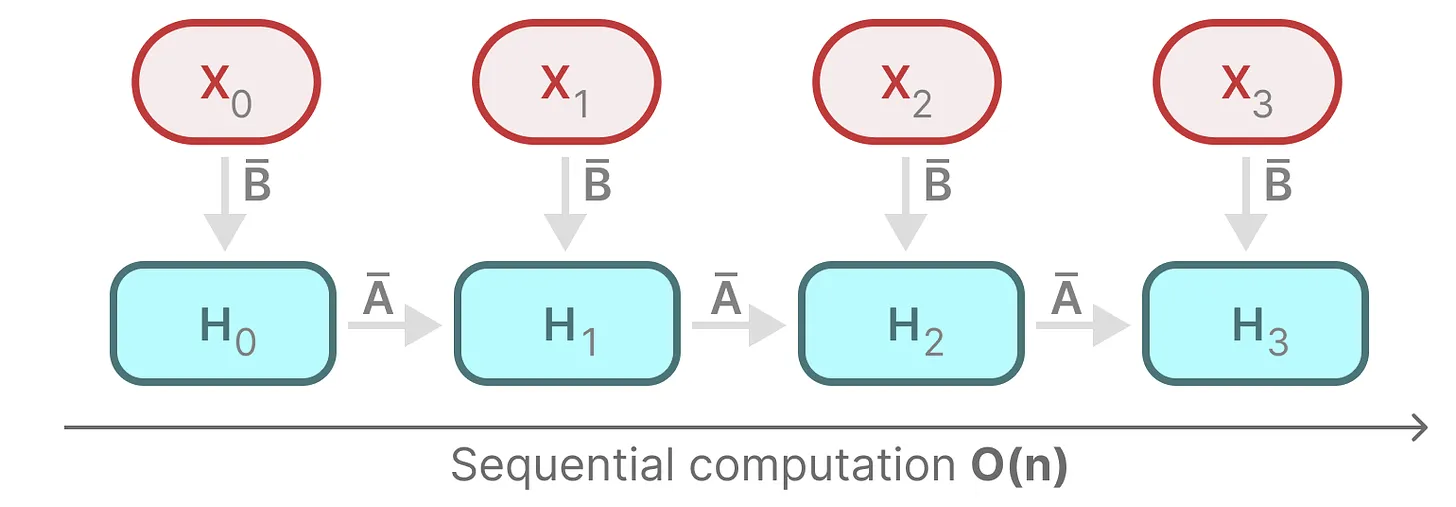
Mamba 通过并行扫描（parallel scan）算法使得最终并行化成为可能，其假设我们执行操作的顺序与关联属性无关。

pscan 是 Belloch 算法 的 pytorch 实现

因此，我们可以分段计算序列并迭代地组合它们，即动态矩阵 \(B\) 和 \(C\) 以及并行扫描算法一起创建选择性扫描算法（selective scan algorithm）。如下图所示：

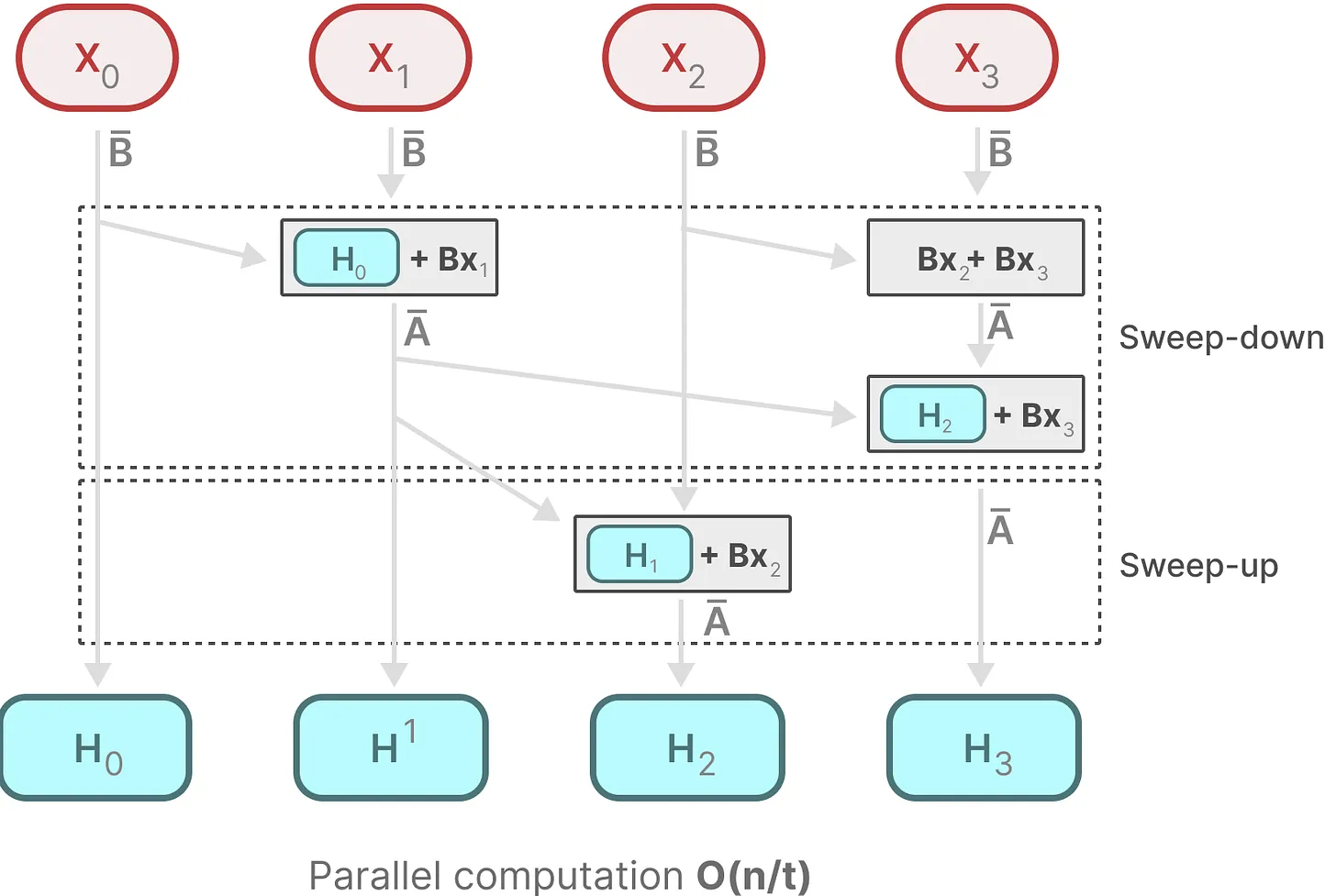
Sweep-down：利用已更新的值更新完剩下的值
Sweep-up：求整个矩阵总和的形式原地更新矩阵值

Flash Attention

此外，为了让传统的 SSM 模型在现代 GPU 上也能高效计算，Mamba 中也使用了 Flash Attention 技术。

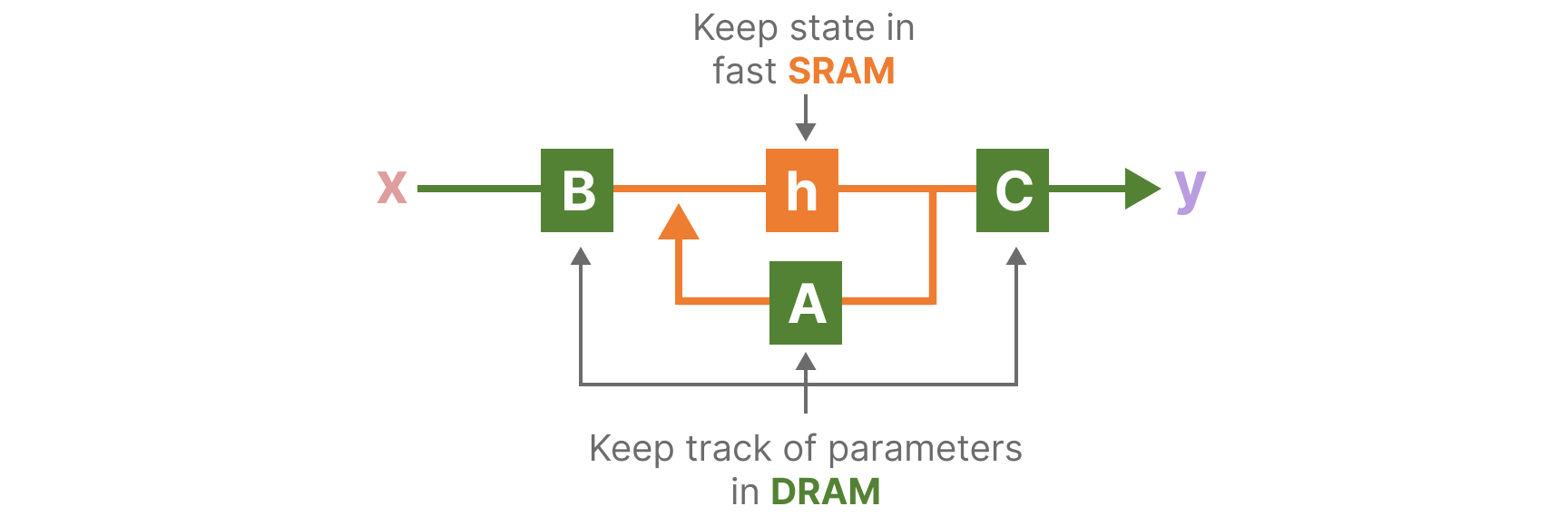
简而言之，利用内存的不同层级结构处理 SSM 模型的状态，减少高带宽但慢速的 HBM 内存反复读写这个瓶颈。

Mamba 借鉴 Flash Attention 的示意图

具体而言，就是限制需要从 DRAM 到 SRAM 的次数（通过内核融合来实现），避免一有个结果便从 SRAM 写入到 DRAM，而是待 SRAM 中有一批结果再集中写入 DRAM 中，从而降低来回读写的次数。

Mamba 在更高速的 SRAM 内存中执行离散化和递归操作，再将输出写回 HBM：

不是在 GPU HBM 中将大小为 \((B,L,D,N)\) 的扫描输入进 (A,B)，而是直接将 SSM 参数 \((\Delta,A,B,C)\) 从慢速 HBM 加载到快速 SRAM 中。
- 注意，当输入从 HBM 加载到 SRAM 时，中间状态不被保存，而是在反向传播中重新计算
然后，在 SRAM 中进行离散化，得到 \((B,L,D,N)\) 的 \(\bar{A},\bar{B}\)
接着，在 SRAM 中进行扫描（通过并行扫描算法），得到 \((B,L,D,N)\) 的输出。
最后，与 \(C\) 进行乘法和假发，得到 \((B,L,D)\) 的最终输出，并重新写回 HBM

简化的 SSM 架构

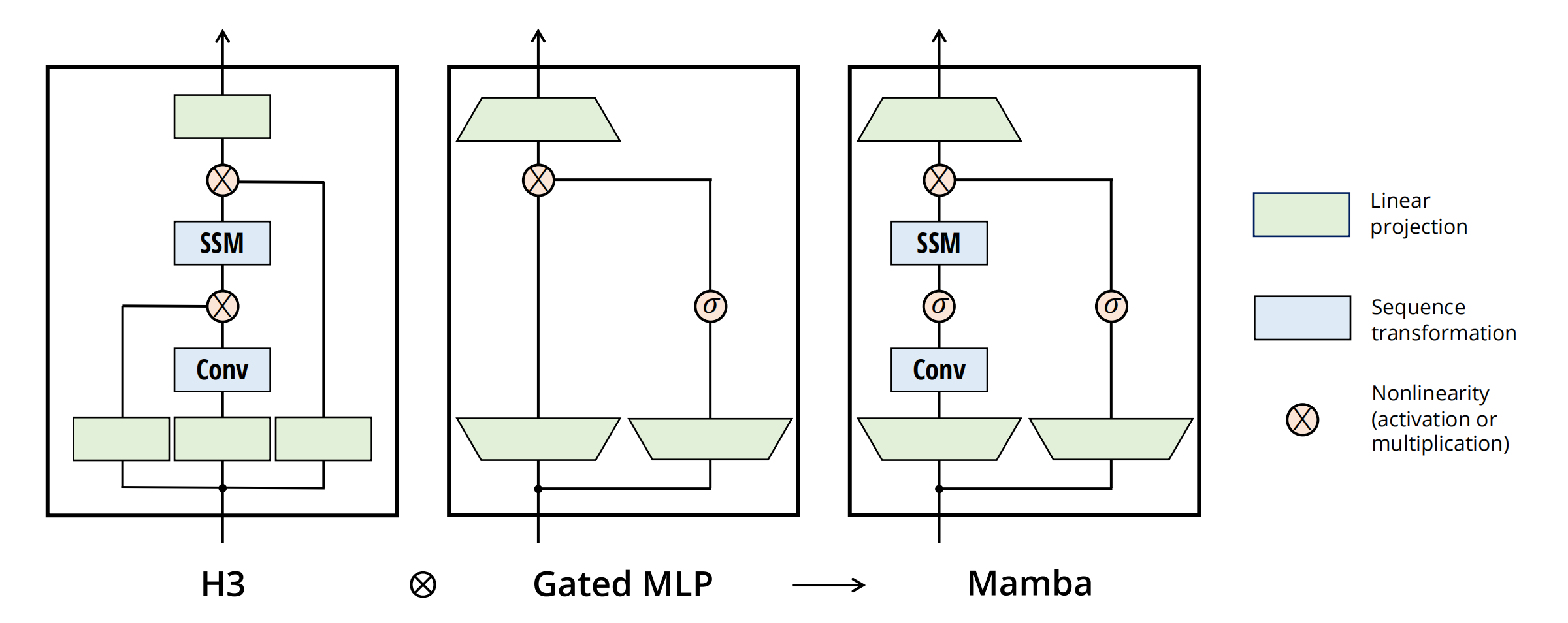
将大多数 SSM 架构（比如 H3）的基础块，与现代神经网络（比如 transformer）中普遍存在的门控 MLP 相结合，组成新的 Mamba 块。重复这个块，并与归一化和残差连接结合，便构成了 Mamba 架构。如下图所示：

Mamba 架构示意图

Vision Mamba

2024.01.17 首次提交 Arxiv
Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model

VMamba

2024.01.18 首次提交 Arxiv
VMamba: Visual State Space Model

总结

参考

论文：
博客：Mamba: The Easy Way
博客：A Visual Guide to Mamba and State Space Models
CSDN：
bilibili：
- 【汇报】 Mamba 模型及其公式推导
Mamba 的最小代码实现：mamba-minimal

文档信息

本文作者：Bookstall
本文链接：https://bookstall.github.io/2024/04/22/state-space-model/
版权声明：自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）

Bookstall