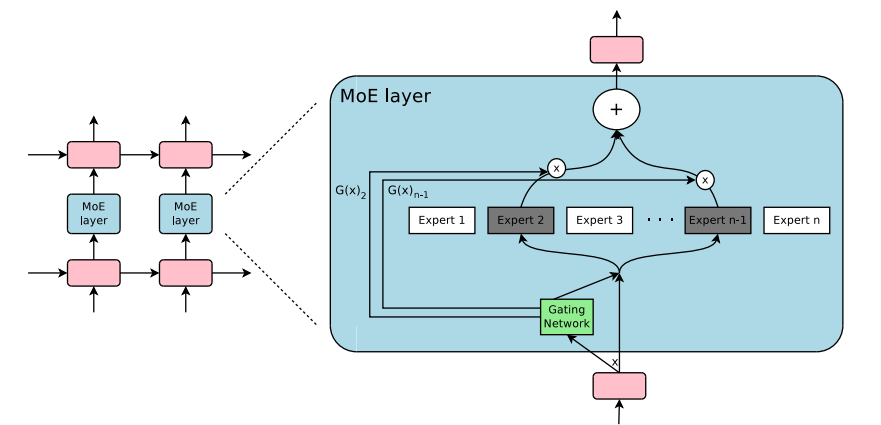
Mixture of Experts(MoE)

Mixtral
基本超越 LLaMA 2 70B
Mixtral 8×7B 在大多数基准测试中都优于 LLaMA2 70B,推理速度快了 6 倍。
它是最强大的、具有宽松许可的开放权重模型,也是最佳性价比之选。
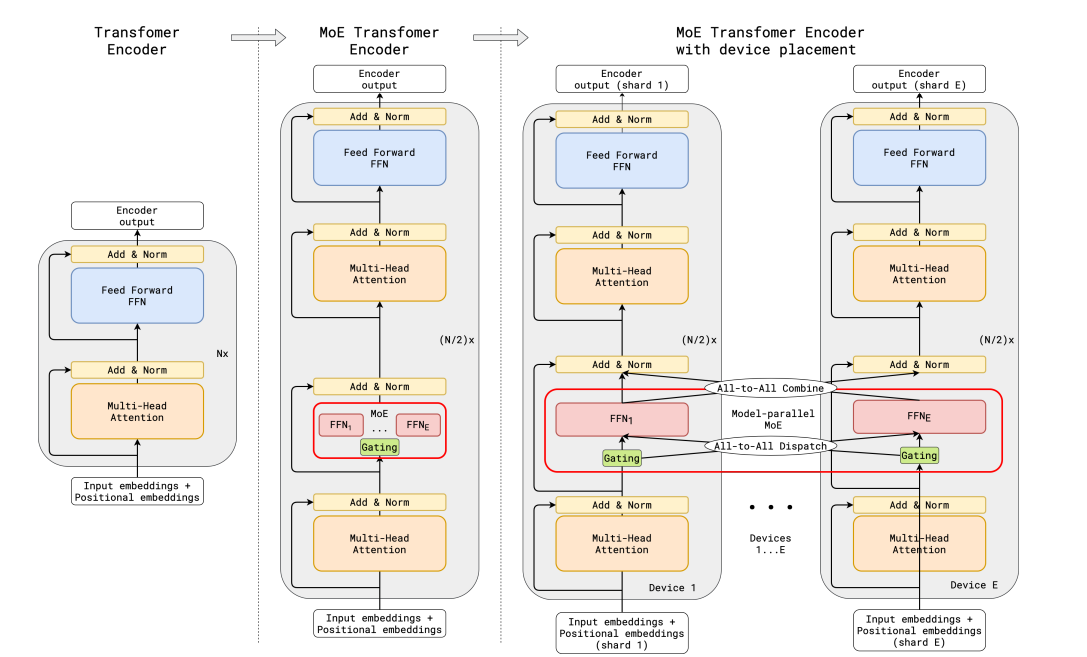
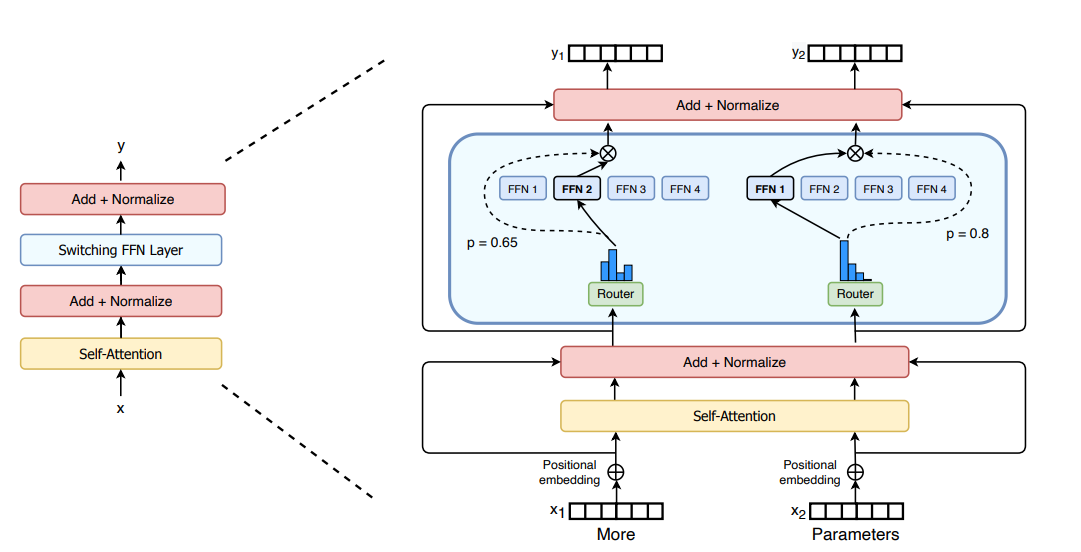
具体来说,Mixtral 采用了稀疏混合专家网络,是一个 decoder-only 的模型。其中,前馈块(FFN)会从 8 组不同的参数组中进行选择。也就是说,实际上,Mixtral 8×7B 并不是 8 个 7B 参数模型的集合,仅仅是 Transformer 中的前馈块(FFN)有不同的 8 份。
这也就是为什么 Mixtral 的参数量并不是 56B,而是 46.7B。
其特点包括以下几个方面:
在大多数基准测试中表现优于 Llama2 70B,甚至足以击败 GPT-3.5
上下文窗口为 32k
可以处理英语、法语、意大利语、德语和西班牙语
在代码生成方面表现优异
遵循 Apache 2.0 许可(免费商用)
具体测试结果如下:

另外,在幻觉问题方面,Mixtral 的表现也优于 LLaMA2 70B:
在 TruthfulQA 基准上的成绩是 73.9% vs 50.2%;
在 BBQ 基准上呈现更少的偏见;
在 BOLD 上,Mixtral 显示出比 LLaMA2 更积极的情绪。
此次与 Mixtral 8×7B 基础版本一起发布的,还有 Mixtral 8x7B Instruct 版本。后者经过 SFT 和 DPO 优化,在 MT-Bench 上拿到了 8.3 的分数,跟 GPT-3.5 差不多,优于其他开源大模型。

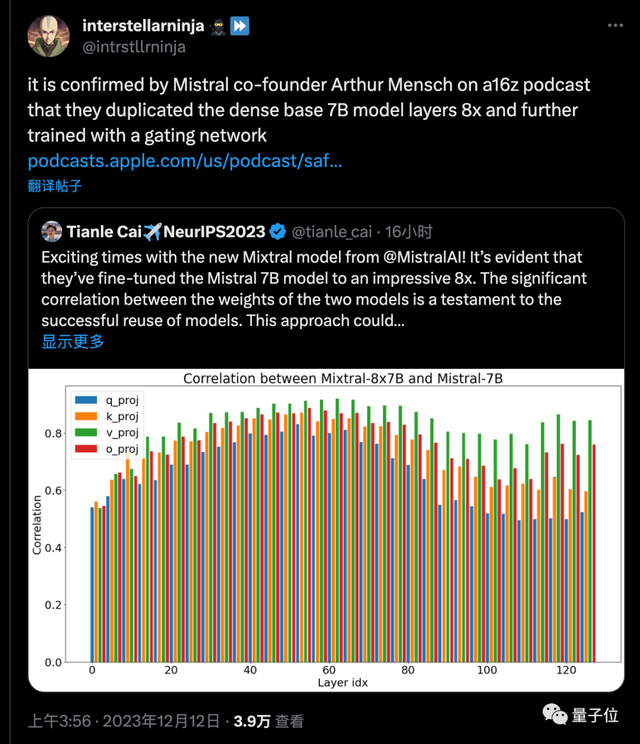
更关键的是,普林斯顿博士生 Tianle Cai分析了 Mistral-7B 与 Mixtral-8x7B 模型的权重相关性做了分析,证明了模型的成功复用。
随后网友发现,Mistral AI 创始人也亲自证实,MoE 模型确实就是把 7B 基础模型复制 8 次,再进一步训练来的。
体验
目前,Mistral 官方已经宣布上线 API 服务,不过还是邀请制,未受邀用户需要排队等待。
值得关注的是,API 分为三个版本:
小小杯(Mistral-tiny):对应模型是 Mistral 7B Instruct;
小杯(Mistral-small):对应模型是这次发布的 Mixtral 8×7B;
中杯(Mistral-medium):对应的模型尚未公布,但官方透露其在 MT-Bench 上的得分为 8.6 分。
而在线版本,目前还只能到第三方平台(Poe、HuggingFace等)体验。
能看懂中文,但不太愿意说
虽然官方通告中并没有说支持中文,但我们实测(HuggingFace Chat 中的在线版,模型为 Instruct v0.1 版本)发现,Mixtral 至少在理解层面上已经具备一定中文能力了。
生成层面上,Mixtral 不太倾向于用中文来回答,但如果指明的话也能得到中文回复,不过还是有些中英混杂的情况。
更新:Mixtral-8x7B 论文发表
论文 Mixtral of Experts 已经发表在 Arxiv 上。详细的论文解决可以参见 一条磁力链爆全网,Mixtral 8x7B 论文来了!碾压 Llama 2 70B,每 token 仅需激活 13B 参数。
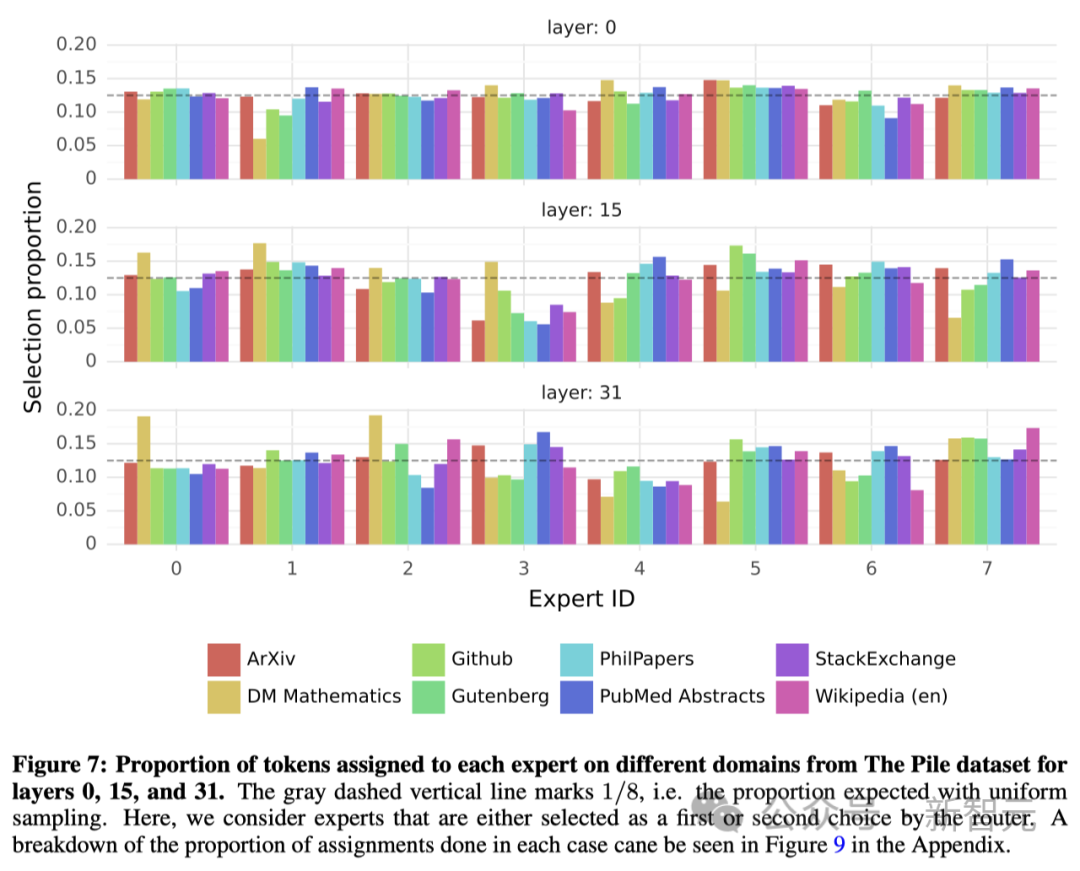
研究人员对路由器如何选择「专家」进行了简要分析。特别是在训练期间,是否会有「专家」选择专攻某些特定的领域(如数学、生物学、哲学等)。为了探究这一点,研究人员对 The Pile 验证数据集的不同子集进行了「专家」选择分布的测量,结果如下图所示。涉及模型的第 0 层、第 15 层和第 31 层(最后一层)。
出乎意料的是,这里并 没有发现明显的基于主题分配「专家」的模式。比如,在所有层中,无论是 arXiv 论文(用 LaTeX 编写)、生物学领域(PubMed 摘要)还是哲学领域(PhilPapers 文件),「专家」的分配分布都非常相似。只有在数学领域(DM Mathematics)中,「专家」的分布略有不同,专家 0 和专家 2 分配的 token 比较多。
研究人员认为,这种差异可能是因为数据集本身是合成的,且对自然语言的覆盖上有限,尤其是在模型的第一层和最后一层,隐藏状态分别与输入和输出嵌入高度相关。而这也表明,路由器确实表现出了一些结构化的句法行为。
各个专家分配的 “比较均匀”
下图展示了不同领域(Python 代码、数学和英语)的文本示例。其中,每个 token 都用不同的背景色标注,便于查看对应分配到的「专家」。

可以发现,像 Python 中的「self」和英文中的「Question」这样的词语,虽然包含有多个 token,但往往被分配给同一个「专家」。同样,相邻的 token 也会被分配给同一位「专家」。
在代码中,缩进的 token 也总是被指派给相同的「专家」,这一点在模型的第一层和最后一层尤为显著,因为这些层的隐藏状态与模型的输入和输出更加紧密相关。此外,在 The Pile 数据集上,研究人员还发现了一些位置上的 邻近性(positional locality)。也就是说,连续的标记通常被分配给相同的专家。
Mixtral 在推理时用到的一些 trick,具体为:
Sliding Window Attention (SWA,滑动窗口 Attention)
Rolling Buffer Cache(也被称为 Rotating Buffer Cache,即旋转式存储的 KV cache)
Long-context Chunking(长上下文场景下的 chunking 策略,配合前两者食用)
0、LLM 推理的两个阶段
一个常规的 LLM 推理过程通常分为两个阶段:prefill 和 decode,如下图所示:
0.1、Prefill
预填充阶段。在这个阶段中,我们 把整段 prompt 喂给模型做 forward 计算。如果采用 KV cache 技术,在这个阶段中我们会把 prompt 过 $W_k、W_v$ 后得到的 $X_k、X_v$ 保存在 cache_k 和 cache_v 中。这样在对后面的 token 计算 attention 时,我们就不需要对前面的 token 重复计算了,可以帮助我们节省推理时间。
在上面的图例中,我们假设 prompt 中含有 3 个 token,prefill 阶段结束后,这三个 token 相关的 KV 值都被装进了 cache。
0.2、Decode
生成 response 的阶段。在这个阶段中,我们根据 prompt 的 prefill 结果,一个 token 一个 token 地生成 response。
同样,如果采用了 KV cache,则每走完一个 decode 过程,我们就把对应 response token 的 KV 值存入 cache 中,以便能加速计算。例如对于图中的 t4,它与 cache 中 t0~t3 的 KV 值计算完 attention 后,就把自己的 KV 值也装进 cache 中。对 t6 也是同理。
由于 Decode 阶段的是逐一生成 token 的,因此它不能像 prefill 阶段那样能做大段 prompt 的并行计算,所以在 LLM 推理过程中,Decode 阶段的耗时一般是更大的。
1、分组查询注意力(GQA)
1.1、引言
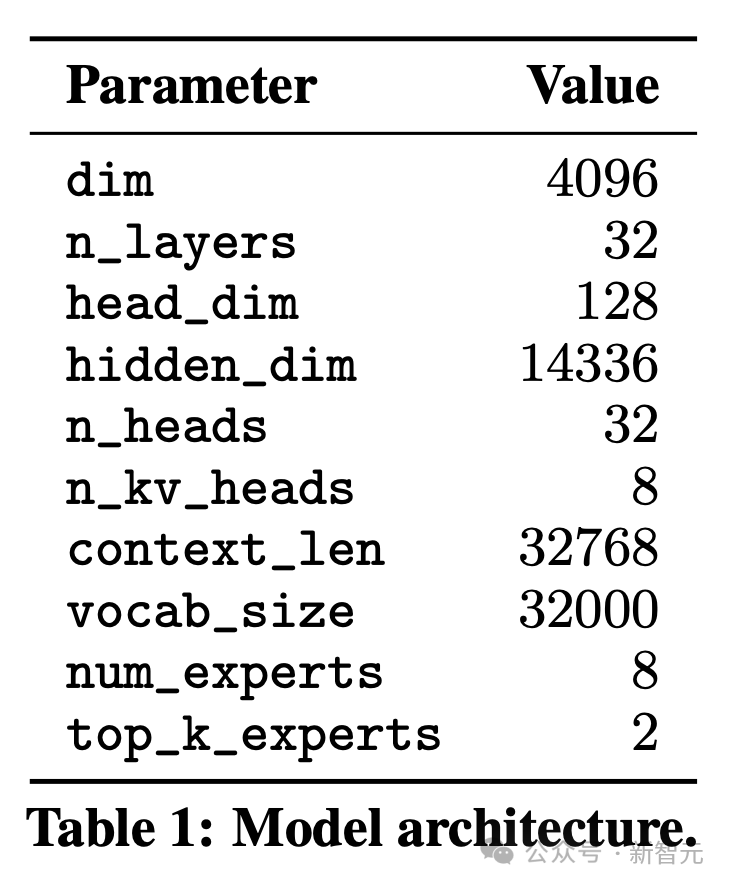
Mistral 7B 对应的论文为 《Mistral 7B》(另,这是 其 GitHub 地址),以下是「模型参数图」

Mistral 7B 在所有评估基准中均胜过了目前最好的 13B 参数模型(Llama 2,对标的第二代),并在推理、数学和代码生成方面超越了 Llama 34B(这里对标 Llama 第一代的 34B,原因是当时 Llama 2 34B 尚未发布)
该模型采用了 分组查询注意力(GQA),GQA 显著加快了推理速度,还减少了解码期间的内存(KV cache)需求,允许更高的批处理大小,从而提高吞吐量
同时结合滑动窗口注意力(sliding window attention,简称 SWA)以有效处理任意长度的序列
SWA 不是 Mistral 的首创,而是基于这两篇论文实现的:Generating Long Sequences with Sparse Transformers、Longformer: The Long-Document Transformer
你再看上上张图所示的「模型参数图」,可知
context_len8192 是说它训练的时候,传进来的数据最大只能到 8192 个 tokens,也就是训练时的上下文长度上限windows_size 4096 是 sliding windows attention 的滑窗大小,1 次 attention 计算的上下文范围只有 4096 个 tokens
言外之意是,每个 token 只最多计算 4096 的范围
第 5000 个 token 只计算 $[905: 5000]$ 这个范围的 attention
第 5001 个 token 只计算 $[906: 5001]$ 这个范围的 attention
位置编码方面,和 Llama 统一用的 RoPE
所以你看上面的「模型参数图」,维度(dim):4096,总计 32 个头(n_heads),每个头的维度(head_dim):128,这一眼可以看出来,而 n_kv_heads 是啥呢?
咋一看好像不太好理解,是不?其实,正是因为 Mistral 用了 GQA,n_heads 指的是 Q 的头数,n_kv_heads 指的是 K、V 的头数

不过要注意的是,与上图中间所示部分不太一样的地方在于:
上图中间所示部分中,
Q的头数是K V头数的 2 倍但在 Mistral 的 GQA 中,
Q的头数是K V头数的 4 倍
实际上,MHA、MQA 可以看做是 GQA 两个特例版本:
MQA 对应 GQA-1,即只有一个分组,对应一个 K 和 V;
MHA 对应 GQA-H,对应 H 个分组,对应 H 个 K 和 V;
1.2、代码实现
参考:
GQA 论文:GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints
- Unofficial Implementation:grouped-query-attention-pytorch
HuggingFace 中 MixtralAttention 的 实现:
通过将
K V的值expand复制到与Q相同的dim数量例如,
n_kv_heads为 8,n_heads为 32,head_dim为 128,那么总共的分组数量
n_kv_groups为 32 // 8 = 4每组
K V的值都需要复制 $4 - 1 = 3$ 次(repeat_kv)
self.hidden_size = config.hidden_size # 128 * 32 = 4096
self.num_heads = config.num_attention_heads # 32
self.head_dim = self.hidden_size // self.num_heads # 4096 // 32 = 128
self.num_key_value_heads = config.num_key_value_heads # 8
self.num_key_value_groups = self.num_heads // self.num_key_value_heads # 32 // 8 = 4
self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=False) # (4096, 4096)
self.k_proj = nn.Linear(self.hidden_size, self.num_key_value_heads * self.head_dim, bias=False) # (4096, 8 * 128) = (4096, 1024)
self.v_proj = nn.Linear(self.hidden_size, self.num_key_value_heads * self.head_dim, bias=False) # (4096, 1024)
self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=False) # (4096, 4096)
query_states = self.q_proj(hidden_states) # Q
key_states = self.k_proj(hidden_states) # K
value_states = self.v_proj(hidden_states) # V
query_states = query_states.view(bsz, q_len, self.num_heads, self.head_dim).transpose(1, 2) # (bs, 32, len, 128)
key_states = key_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim).transpose(1, 2) # (bs, 8, len, 128)
value_states = value_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim).transpose(1, 2) # (bs, 8, len, 128)
# repeat k/v heads if n_kv_heads < n_heads
key_states = repeat_kv(key_states, self.num_key_value_groups) # (bs, (1 + 3) * 8, len, 128) = (bs, 32, len, 128)
value_states = repeat_kv(value_states, self.num_key_value_groups) # (bs, 32, len, 128)
# (bs, 32, len, 128) * (bs, 32, 128, len) = (bs, 32, 128, 128)
attn_weights = torch.matmul(query_states, key_states.transpose(2, 3)) / math.sqrt(self.head_dim)
# upcast attention to fp32
attn_weights = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(query_states.dtype) # (bs, 32, 128, 128)
attn_weights = nn.functional.dropout(attn_weights, p=self.attention_dropout, training=self.training)
attn_output = torch.matmul(attn_weights, value_states) # (bs, 32, 128, 128) * (bs, 32, len, 128) = (bs, 32, len, 128)
attn_output = attn_output.transpose(1, 2).contiguous() # (bs, len, 32, 128)
attn_output = attn_output.reshape(bsz, q_len, self.hidden_size) # (bs, len, 32 * 128) = (bs, len, 4096)
attn_output = self.o_proj(attn_output) # (bs, len, 4096)
repeat_kv 函数的实现如下所示:
def repeat_kv(hidden_states: torch.Tensor, n_rep: int) -> torch.Tensor:
"""
This is the equivalent of torch.repeat_interleave(x, dim=1, repeats=n_rep). The hidden states go from (batch,
num_key_value_heads, seqlen, head_dim) to (batch, num_attention_heads, seqlen, head_dim)
"""
batch, num_key_value_heads, slen, head_dim = hidden_states.shape
if n_rep == 1:
return hidden_states
hidden_states = hidden_states[:, :, None, :, :].expand(batch, num_key_value_heads, n_rep, slen, head_dim)
return hidden_states.reshape(batch, num_key_value_heads * n_rep, slen, head_dim)
使用 einops 库的实现:
import torch
import torch.nn.functional as F
from einops import einsum, rearrange
dim = 4096
head_dim = 128
n_heads = 32
n_kv_heads = 8
n_kv_groups = n_heads // n_kv_heads
batch_size = 1
seq_len = 256
query = torch.randn(batch_size, seq_len, n_heads, head_dim)
key = torch.randn(batch_size, seq_len, n_kv_heads, head_dim)
value = torch.randn(batch_size, seq_len, n_kv_heads, head_dim)
scale = query.size(-1) ** 0.5 # 缩放因子
query = rearrange(query, "b l h d -> b h l d")
key = rearrange(key, "b s h d -> b h s d")
value = rearrange(value, "b s h d -> b h s d")
# split query n_heads in groups
# 将 query 进行分组
query = rearrange(query, "b (h g) l d -> b g h l d", g=n_kv_groups)
# calculate the attention scores and sum over the group dim to perform averaging
scores = einsum(query, key, "b g h l d, b h s d -> b h l s")
attention = F.softmax(scores / scale, dim=-1)
# apply weights to the value head
out = einsum(attention, value, "b h l s, b h s d -> b h l d")
# reshape back to original dimensions
out = rearrange(out, "b h l d -> b l h d")
2、Sliding Window Attnetion(SWA):扩展上下文长度
2.1、引言
从第一部分的介绍中,我们应该能感受到一点:LLM 推理中的 KV cache 加速法,是非常典型的用 “空间换时间” 的操作。随着 seq_len 变长,cache 中存储的数据量也越来越大,对显存造成压力。
所以,我们自然而然想问:有什么办法能减缓 cache 的存储压力呢?
注意到,cache 的存储压力之所以变大,是因为我们的 Attention 是 causal decoder 形式的,即每一个 token 都要和它之前所有的 token 做 Attention,所以 cache 中存储的数据量才和 seq_len 正相关。
如果现在我们转换一下思路,假设每一个 token 只和包含其本身在内的前 $W$ 个 token 做 Attention,这样不就能把 cache 的容量维持在 $W$ 吗?而从直觉上来说,这样的做法也有一定的道理:对当前 token 来说,距离越远的 token,能提供的信息量往往越低,所以似乎没有必要浪费资源和这些远距离的 token 做 Attention。
这种 Attention 思路的改进,就被称为 Sliding Window Attention(SWA),其中 $W$ 表示窗口长度。这也是 Mixtral 7b 和 Mixtral 8 * 7b 采用的方法,我们通过作者论文中的一张图,更清晰地来看下它和传统 Attention 的区别,这里 $W=3$。
2.2、为什么能用滑动窗口
虽然滑动窗口的策略看起来很不错,不过你一定有这样的疑惑:虽然距离越远的 token 涵盖的信息量可能越少,但不意味着它们对当前 token 一点用处都没有。
在传统的 Attention 中,我们通过 Attention score,或多或少给这些远距离的 token 一定的参与度;但是在 Sliding Window Attention 中,却直接杜绝了它们的参与,这真的合理吗?
为了回答这个问题,我们来看一个例子,在本例中 W=4,num_layers = 4,num_tokens = 10。
我们从 layer3 最后一个位置的 token(t9)看起:
对于 layer3 t9,它是由 layer2 t9 做 sliding window attention 得来的。也就是 layer3 t9 能看到 layer2 t6 ~ t9的信息
再来看 layer2 t6,它能看到 layer1 t3 ~ t6 的信息。也就是说对于 layer3 t9,它最远能看到 layer1 t3 这个位置。
以此类推,当我们来到 layer0 时,不难发现,对于 layer3 t9,它最远能看到 layer0 t0 这个位置的信息。
欸你发现了吗!对于 layer3 t9,虽然在每一层它 “最远” 只能看到前置序列中部分token,但是只要模型够深,它一定能够在某一层看到所有的前置 tokens。
如果你还觉得抽象,那么可以想想 CNN 技术中常谈的 “感受野”。当你用一个固定大小的卷积窗口,对一张原始图片做若干次卷积,得到若干张特征图。越深的特征图,它的每一个像素点看到的原始图片的范围越广。类比到我们的滑动窗口 Attention 上,从 layer0 开始,每往上走一层,对应 token 的感受野就往前拓宽 $W$。
所以,Silding Window Attention 并非完全不利用窗外的 token 信息,而是随着模型层数的增加,间接性地利用起窗口外的 tokens。
2.3、Mask 代码实现
我们知道在LLM推理时,一般分为 Prefill 和 Decode 两个阶段,为了满足 SWA,Prefill 阶段可以通过一个 mask 的掩码操作实现,如下:
if input_ids.shape[1] > 1:
# seqlen推理时在prompt阶段为n,在generation阶段为1
seqlen = input_ids.shape[1]
# mask在推理时也只在prompt阶段有,
#定义一个全1方阵
tensor = torch.full((seqlen, seqlen),fill_value=1)
# 上三角部分全为0
mask = torch.tril(tensor, diagonal=0).to(h.dtype)
# make the mask banded to account for sliding window
# 这里代码diagonal应该等于(-self.args.sliding_window+1)才能满足window size为
# self.args.sliding_window,这应该是官方代码的一个小bug?
mask = torch.triu(mask, diagonal=-self.args.sliding_window)
mask = torch.log(mask)
"""
举个例子,tensor.shape : [10,10]
self.args.sliding_window = 5,则mask为
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 1, 0, 0, 0],
[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 1, 1, 1, 1, 1, 1]])
"""
3、滚动缓冲区缓存(Rolling Buffer Cache)
3.1、原理
当我们使用滑动窗口后,KV Cache 就不需要保存所有 tokens 的 KV 信息了,你可以将其视为一个固定容量($W$)的 cache,随着 token index 增加,我们来 “滚动更新” KV Cache。
类似 循环队列 的数据结构
下图给出了 Rolling Buffer Cache 的运作流程:
在图例中,我们做推理时喂给模型一个 batch_size = 3 的 batch,同时设 $W = 3$。此时 KV Cache 的容量为 (batch_size, W)。我们以第 1 条 prompt This is an example of ... 为例:
在 $i$ 时刻,我们对
an做 attention,做完后将an的 KV 值更新进 cache 中在 $i + 1$ 时刻,我们对
example做 attention,做完后将example的 KV 值更新进 cache 中。此时对于第 1 条 prompt,它在 KV cache 中的存储空间已满。在 $i + 2$ 时刻,我们对
of做attention,由于此时 KV cache 已满,所以我们将of的 KV 值更新进 KV cache 的 $0$ 号位置,替换掉原来This的 KV 值。再后面时刻的 token 也以此类推。
不难发现,prompt 中第 $i$ 个 token 在 KV cache 中的存储序号为:i % W。
3.2、“旋转” 从何而来
如果你读过 Mixtral 的源码,你可能会记得,在源码中管 Rolling Buffer Cache 叫Rotary Buffer Cache。而 “Rotary” 这个词很值得我们关注:为什么叫 “旋转” 呢?
我们再回到 3.1 的图例中:
还是对于第一条数据,我们往上添两个单词,假设其为 This is an example of my last...。现在来到了单词 last 上,我们需要对它计算 Sliding Window Attention。
不难理解,在 $W=4$ 的情况下,last 的 Attention 和 example of my last 相关。现在我们把目光放到图中的 KV Cache 上:它的存储顺序似乎不太对,如果我们想对 last 做 Attention,就要对当前 KV Cache 中存储的元素做一次 “旋转”,将其转回正确的位置。
所以,Rotary 的意思就是:通过某种规则,将 Cache 中的数据旋转回正确的位置,以便能正确做 Attention。这个规则在 Mixtral 源码中用一个 unrotate 函数来定义。在后文我们会详细看这个函数的运作方式。
3.3 代码实现
RotatingBufferCache 代码实现如下:
# The cache is a rotating buffer
# positions[-self.sliding_window:] 取最后w个位置的索引,取余
# [None, :, None, None]操作用于扩维度[1,w,1,1]
scatter_pos = (positions[-self.sliding_window:] % self.sliding_window)[None, :, None, None]
# repeat操作repeat维度 [bsz, w, kv_head, head_dim]
scatter_pos = scatter_pos.repeat(bsz, 1, self.n_kv_heads, self.args.head_dim)
# src取[:,-w,:,:] 所以src.shape=[bsz,w,kv_head,head_dim]
# 根据scatter_pos作为index 将src写入cache
self.cache_k[:bsz].scatter_(dim=1, index=scatter_pos, src=xk[:, -self.sliding_window:])
self.cache_v[:bsz].scatter_(dim=1, index=scatter_pos, src=xv[:, -self.sliding_window:])
4、预填充与分块(chunk):减少重复计算
在生成序列时,需要一个一个地预测token,因为每个token都以前面的token为条件。然而,prompt是提前知道的,可以用prompt预填充(k, v)缓存,即
如果prompt非常大,可以把它分成更小的块,用每个块预填充缓存。为此,可以选择窗口大小作为分块大小。因此,对于每个块,需要计算缓存和块上的注意力 下图展示了注意力掩码在缓存和分块上的工作原理

在预填充缓存时,长序列被分块,以限制内存使用。
我们把一个序列分成三个块来处理,“The cat sat on”,“the mat and saw”,“the dog go to”。上图中显示了第三块(“the dog go to”)发生的情况:它使用因果掩码(最右块)来关注自己,使用滑动窗口(中心块)来关注缓存,并且不关注过去的 token,因为它们在滑动窗口之外(左块)。
Chunking 推理全流程图解
我们用图解的方式把整个推理流程串一遍,好知道代码在做一件什么事情。
1、输入数据
假设推理时 batch_size = 3,且有 chunk_size = cache_size = sliding_window = 4,则这个 batch 的 prompts 可表示成下图(每个方块表示 $1$ 个 token,同色方块属于同个 prompt):
2、chunk-0
我们首先将 chunk-0 送入模型,此时 KV cache 为空。
对 chunk 中的每个 token 计算 Xq,Xk,Xv,用于计算 SWA(Sliding Window Attention)。图中刻画了计算时用到的 mask 矩阵。在 Mixtral 源码中使用 Xformers 库的相关 API 来完成 Attention 相关的计算(这个库的好处是加速 Attention 计算)。
BlockDiagonalCausalMask(全称是 BlockDiagonalCausalLocalAttentionMask)是这个库下提供的一种 mask 方法,它可以这样理解:
block:将矩阵进行分块(block),之后在每一个块内 单独 做 Attention 计算
diagonal causal:每一个 block 内做对角线 mask
Xformers 官方文档在这一块的介绍不太全面,对初次使用 Xformers 的朋友其实不太友好,所以在这里我做了可视化,方便后续大家对代码的理解。
chunk-0 的 SWA 计算完毕后,我们将每个 token 对应的 Xk, Xv 值存入 cache。在源码中,我们会通过一个规则确定每个 token 的 KV 值在 KV cache 中的存储位置,这样也方便我们做 unrotate 操作时能把 cache 中存储的元素旋转回正确的位置。
最后,对于 KV cache,它的 position 序号 的排布顺序是从左至右,从上到下的,即:
Cache position index:
0 | 1 | 2 | 3
4 | 5 | 6 | 7
8 | 9 | 10 | 11
3、chunk-1
对于 chunk-1 中维护的 tokens,我们正常计算他们的
xq,xk,xv。取出当前 KV Cache 中存储的 KV 值,和 chunk-1 计算出来的 KV 值进行拼组,计算 SWA(如图所示,mask 矩阵的 row 行,每个色块由两部分组成:当前cache + 当前 chunk)
在计算 SWA 的 mask 矩阵时,我们同样采用 Xformers 库,这时调用的是
BlockDiagonalCausalLocalAttentionFromBottomRightMask类,和 chunk-0 调用的BlockDiagonalCausalLocalAttentionMask相比,它的主要不同在 “FromBottomRight” 上,也就是对于每个 block,它从右下角开始以窗口长度为 $W$(本例中 $W=4$)的形式设置 mask 矩阵。计算完 chunk-1 的 SWA 后,我们将 chunk-1 的 KV 值更新进 KV Cache 中
4、chunk-2
最后我们来看 chunk-2,这个 chunk 比较特殊,因为在这个 chunk 内,每一个 prompt 维护的序列长度是不一样的,3 个 prompt 维护的 tokens 分别为 [[8, 9, 10, 11], [8, 9], [8]]。
同样,我们计算 chunk-2 的每个 tokens 的
Xq,Xk,Xv取出当前 KV cache,与 chunk-2 的相关结果做 Attention 计算,依然是采用 Xformers 的
BlockDiagonalCausalLocalAttentionFromBottomRightMask类把 chunk-2 计算的 KV 结果更新进 KV Cache。我们特别关注第 2、3 条 prompt(绿红色块)更新后的 KV cache 结果。
rolling buffer cache 设置的放置方式,这两条 prompt 中 KV 值是非顺序存放的。例如对于第 2 条 prompt,它 KV 值的存放顺序是
[8, 9, 6, 7]。因此如果我们想继续对它做 decode,就要把 KV cache 的值unrotate回[6, 7, 8, 9],以此类推。
事实上,无论是 prefill 还是 decode,无论是哪个 chunk,只要涉及到用当前 cache 和 chunk(在 decode 阶段则是 token)做 attention 计算,我们都需要把 cache 中的 KV 值排布 unrotate 一遍。unrotate 的结果就是,如果 cache 中的值已经是按顺序排布的,那就照常输出;如果是非顺序排布的,那就排好了再输出。
由于在 Mixtral 源码中,这块数据处理逻辑比较复杂,又没有写注释,所以很多朋友读到
unrotate的部分可能一头雾水。因此这里特地画出,帮助大家做源码解读。
chunk_size != W 的情况
在前文我们说过,一般设 chunk_size = cache_window = sliding_window,我们也说过这个设置并不绝对,一般 cache_window 和 sliding_window 相等,但是 chunk_size 却不一定要和它们相等。
所以我们来看一个 chunk_size 和其余两者不等的例子。在这个例子中,chunk_size = 5, cache_window = sliding_window = 3
对于每个 chunk 都主要分成三个阶段:更新前的 KV Cache,SWA,更新后的 KV cache。其中前两个阶段和之前的示例差别不大,我们主要来关注下第三个阶段:更新 KV Cache。
不难理解,对于每个 chunk 来说,只有倒数 $W$ 个 token 的 KV 值才应该进 KV cache。例如对 prompt 0 的 chunk-0,我们自然而然会认为用它更新 KV cache 后,KV cache 中 token 的排布应该是 [2, 3, 4],但真的是这样吗?
上图显示了 prompt 0 的不同 chunk 更新 KV cache 后的结果,可以发现:
chunk-0 更新 KV cache 后,元素的排布方式是
[3,4,2](而不是我们认为的[2,3,4]);chunk-1 更新 KV cache 后,元素的排布方式是
[9, 7, 8](而不是我们认为的[7, 8, 9])。
这是因为整个更新过程严格遵循第三部分的 Rolling Buffer Cache 的更新原则(这样我们才能使用一套 unrotate 准则应对 chunk_size 等于和不等于 cache_window/sliding_window 的情况)。详细的更新过程已经在图例中画出。
同样,我们每次在使用 KV Cache 计算 Attention 时,也要注意用 unrotate 方法将 KV Cache 中的元素先按顺序排布好。
一些关于源码的 hint
在写这篇文章时,本来是打算把源码一起讲的。但是写到这里发现,其实代码中最难理解的部分,在这篇文章中已经做了可视化了,剩下的代码细节对读者们来说应该没难度。在这里再给一些 hint(应该也是读者最难理解的 part):
代码中的
RotatingBufferCache类,用来定义一个 KV cache。从始至终只有 1 个 KV cache(或理解成 1 个 cache_k + 1 个 cache_v),它在 prefill 和 decode 阶段不断被更新代码中
CacheView类,用来操作 KV cache(正如它的命名一样,它是 cache 的视图)。如果说RotatingBufferCache用来管理 cache 的结构,那么CacheView则对 cache 中的具体数据进行更新、排序等操作。代码中
RotatingCacheInputMetadata类,用来定义如何生成当前 chunk 的 KV cache 信息。从上面的例子中我们知道,当前 chunk 计算出的 KV 值是要被更新进 KV cache 中的,那么 chunk 中的哪些 token 要被更新进 KV cache 中(例如chunk_size != sliding_window/cache_window时,只有倒数 $W$ 个 token 要被更新进 KV cache 中)?这些 token 的 KV 值在 cache 中要存放在什么位置?诸如此类的信息,我们都在RotatingCacheInputMetadata中定义。代码中
unrotate方法,用来定义如何把 KV cache 中的元素正确排布,以便做 Attention代码中
interleave_list方法,用来定义 Attention mask 矩阵中的 col 方向元素排布(例如5.2(2)中的中间部分的图)。interleave 是 “交织” 的意思。什么是 “交织” 呢?就是 prompt 0 cache + prompt 0 chunk + prompt 1 cache + prompt 1 chunk + prompt 2 cache + prompt 2 chunk 这样插入式交替排布的意思。
MoE
TODO
Load Balance
TODO
路由负载均衡的实现来自 Switch Transformers
Mixtral 8x7B 参数量计算
TODO
参考
HuggingFace:
Mistral
GitHub:https://github.com/mistralai/megablocks-public
Mistral 7B
论文:Mistral 7B
博文:Mistral 7B
代码:https://github.com/mistralai/mistral-src
量子位:
文档信息
- 本文作者:Bookstall
- 本文链接:https://bookstall.github.io/2023/12/13/mixtral-moe/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)