本文主要借鉴苏剑林大佬的博客 《梯度视角下的LoRA：简介、分析、猜测及推广》，侵删！

随着 ChatGPT 及其平替的火热，各种参数高效（Parameter-Efficient）的微调方法也 “水涨船高”，其中最流行的方案之一就是本文的主角 LoRA 了，它出自论文 《LoRA: Low-Rank Adaptation of Large Language Models》。

能否从优化器角度来分析和实现 LoRA 呢？本文就围绕此主题展开讨论。

1、LoRA 简介

以往的一些结果（例如 《Exploring Universal Intrinsic Task Subspace via Prompt Tuning》）显示，尽管预训练模型的参数量很大，但每个下游任务对应的 本征维度（Intrinsic Dimension） 并不大，换句话说，理论上我们可以 微调非常小的参数量，就能在 下游任务 取得不错的效果。

为了与 LoRA 原始论文中的符号一致，这里还是使用符号 \(A, B\)，而非像苏剑林大佬博客 《梯度视角下的LoRA：简介、分析、猜测及推广》 中使用符号 \(U, V\)

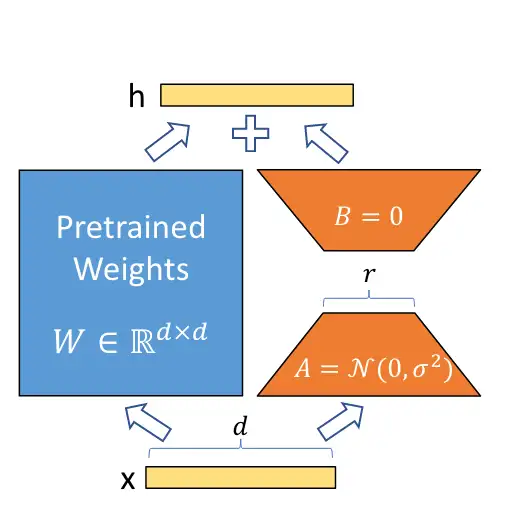
LoRA 借鉴了上述结果，提出对于预训练的参数矩阵 \(W_0\in\mathbb{R}^{m\times n}\)，不去直接微调 \(W_0\)，而是对 增量 做 低秩分解，即：

其中，\(A, B\) <p style="color:red">之一</p>使用全零初始化；\(W_0\) 固定不变；优化器只优化 \(A, B\)。

由于本征维度很小的结论，所以 \(r\) 我们可以取得很小，很多时候我们甚至可以直接取 \(1\)。所以说，LoRA 是一种参数高效的微调方法，至少被优化的参数量大大降低了。

2、梯度分析

正如《Ladder Side-Tuning：预训练模型的“过墙梯”》所提到的，很多参数高效的微调实际上只是降低了显存需求，并没有降低计算量，LoRA 其实也不例外。为了认识到这一点，我们只需要观察 \(A,B\) 的梯度：

其中，\(\mathcal{L}\) 是损失函数，并且 约定参数的 shape 跟其梯度的 shape 一致。

在训练过程中，求模型梯度是主要的计算量，如果全量更新，那么所用的梯度是 \(\frac{\partial \mathcal{L}}{\partial W}\)，而 LoRA 所用的梯度则是 \(\frac{\partial \mathcal{L}}{\partial A}\) 和 \(\frac{\partial \mathcal{L}}{\partial B}\)，它们是建立在全量更新的梯度 \(\frac{\partial \mathcal{L}}{\partial W}\) 基础上的，所以理论上 LoRA 的计算量比全量更新还大。

那为什么实际使用时 LoRA 的训练速度也会变快呢？有如下几个原因：

• 只更新了部分参数：比如 LoRA 原论文就选择只更新 Self Attention 的参数矩阵 \(W_q, W_v\)，实际使用时我们还可以选择只更新其他层的参数（例如 AdaLoRA 论文 中的实验表明，更新参数矩阵 \(W_q, W_k, W_v, W_{f_1}, W_{f_2}\) 能够进一步提升模型性能）；

• 减少了通信时间：由于更新的参数量变少了，所以（尤其是多卡训练时）要传输的数据量也变少了，从而减少了传输时间；

• 采用了各种低精度加速技术，如 FP16、FP8 或者 INT8 量化等；

这三部分原因确实能加快训练速度，然而它们并不是 LoRA 所独有的，事实上几乎都有参数高效方法都具有这些特点。LoRA 的优点是它的 低秩分解很直观，在不少场景下跟全量微调的效果一致，以及在预测阶段可以直接把 \(W_0,A,B\) 合并成单个矩阵从而不增加推理成本。

3、优化器视角

事实上，上面的梯度公式 \(\eqref{eq:grad}\) 也告诉了我们如何从优化器角度来实现 LoRA。

优化器可以直接获取到全量梯度 \(\frac{\partial \mathcal{L}}{\partial W}\)，然后只需要按照公式 \(\eqref{eq:grad}\) 对梯度进行投影，就能够得到 \(A, B\) 的梯度。接着，按照常规的优化器的优化过程来对 \(A, B\) 进行更新。

假设优化器是 SGD，那么优化的过程就是：

由于 \(W_t = W_0 + A_t B_t\)，则 \(W_0 = W_t - A_t B_t\)，然后将 \(W_0\) 代入上式 \(W_{t+1} = W_0 + A_{t+1}B_{t+1}\) 即可

如果是 Adam 之类的带滑动变量的优化器，则 只需要滑动投影后的梯度，因此降低了优化器的参数量，节省了一定的显存。模型越大，这部分参数所占的显存比例也就越大。

4、对称的初始化

LoRA 约定 \(A\) 或 \(B\) 之一使用全零初始化，这是 为了保证初始状态模型跟预训练一致，但同时也带来了不对称问题（一个全零，一个非全零）。事实上，\(A,B\) 都使用 非全零初始化 也是可以的，只需要事先将预训练权重减去 \(A_0 B_0\) 就行了，或者等价地说，将 \(W\) 参数化为：

这样同时保持了初始状态一致，同时允许 \(A,B\) 都用非全零初始化，增强了对称性。

5、随机投影

如果我们将 SGD 场景下的更新量 \(A_{t+1} B_{t+1} − A_t B_t\) 展开，结果将是

假设 \(\eta^2\) 项是可以忽略的高阶项，那么就剩下

从这个角度来看，相比全量微调的 SGD，LoRA 就是用括号中的结果替代了全量的梯度 \(\frac{\partial \mathcal{L}}{\partial W_t}\)。

简单起见，接下来我们只关心 \(r=1\) 的情形，留意到在上式中，\(t\) 时刻的投影向量 \(A_t,B_t\) 是依赖于 \(t\) 的，如果我们将它们换成不依赖于 \(t\) 的随机向量（每步训练都重新随机生成），那么会发生什么呢？

我们考虑 \(a,b∼\mathcal{N}(0,1)\)，其中 \(a\in R^{m\times 1}, b\in R^{1\times n}\)，那么更新量就变为

可以证明的是：

这里的 \(I_{m\times m},I_{n\times n}\) 分别指 \(m\times m,n\times n\) 的单位矩阵。因此，跟 “零阶梯度” 类似，在平均意义下，这种每步都重新初始化的 LoRA 事实上等价于满秩的 SGD。然而，真要按照这个方式实现的话，其速度甚至可能比满秩的 SGD 都要慢，所以它的目的不是提速，而是希望能 缓解灾难遗忘问题——通过对单个（batch）样本使用低秩矩阵（而不是满秩）更新量的方式，减少对整个模型权重的影响。

当然，这只是猜测，实际效果如何，笔者还没有实验过。

6、变体：加性低秩分解

同样还是先只考虑 \(r=1\) 的情形，LoRA 相当于假设了 \(\Delta w_{i,j} = a_i b_j\)，我们能不能做其他低秩分解假设呢？比如 \(\Delta w_{i,j} = a_i + b_j\)？写成矩阵形式就是

其中 \(\mathbb{1}_{1\times n},\mathbb{1}_{m\times 1}\) 分别指 \(1\times n,m\times 1\) 的全 1 矩阵。

容易求出它的梯度是：

其实就是原本梯度的行求和（\(\frac{\partial \mathcal{L}}{\partial A}\)）与列求和（\(\frac{\partial \mathcal{L}}{\partial B}\)）。

相比原版 LoRA，这个加性分解有两个优点：

• 加比乘 计算量更低，梯度 形式也更简单；

• \(A B\) 的秩一定是 1，但是 \(U \mathbb{1}_{1\times n} + \mathbb{1}_{m\times 1} V\) 的秩可能是 2。如果秩代表了模型能力的话，那也就是说同样的参数量，加性的表达能力可能还更强。

FedPara 论文 里有用两个矩阵的 Hadamard 积来做分解的方法，用两个 \(m×R\) 和 \(r×n\) 的矩阵可以达到最高 \(r^2\) 的秩。不过，计算量上倒是比加性要大些。

至于具体效果如何，后面笔者用到 LoRA 的时候，再做对比实验吧。

那么，加性分解能不能 推广 到 \(r>1\) 的情形呢？自然是可以的，但稍微有些技巧。这里约定 \(m,n\) 都能被 \(r\) 整除，那么我们只需要将参数化方式改为

这里的 \(I_{r(1\times n/r)}\)、\(I_{r(m/r\times 1)}\) 分别指 \(1\times n/r\)、\(m/r\times 1\) 的分块矩阵，每一块则是 \(r\times r\) 的单位阵。

这个形式说白了，就是分别将 \(A\)、\(B\) 看成是 \(m/r\times 1\)、\(1\times n/r\) 的分块矩阵，然后套用 \(r=1\) 的思路来操作。

参考

• 苏剑林博客

  • 梯度视角下的LoRA：简介、分析、猜测及推广