前言

众所周知，现在的 Transformer 越做越大，但这个 “大” 通常是 “宽” 而不是 “深”，像 GPT-3 虽然参数有上千亿，但也只是一个 96 层的 Transformer 模型，与我们能想象的深度相差甚远。是什么限制了 Transformer 往 “深” 发展呢？

可能有的读者认为是算力，但 “宽而浅” 的模型所需的算力不会比 “窄而深” 的模型少多少，所以算力并非主要限制，归根结底还是 Transformer 固有的训练困难（如下图所示）。一般的观点是，深模型的训练困难源于梯度消失或者梯度爆炸，然而实践显示，哪怕通过各种手段改良了梯度，深模型依然不容易训练。

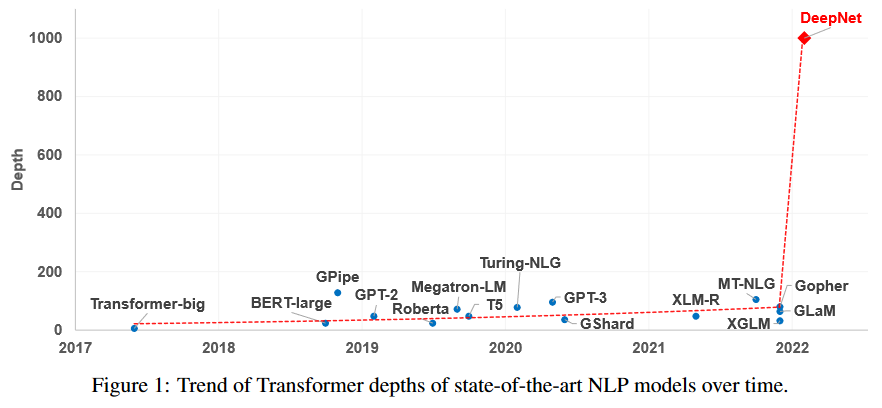
近来的一些工作（如 Admin）指出，深模型训练的根本困难在于 “增量爆炸”，即模型越深对输出的扰动就越大。

上周的论文 《DeepNet: Scaling Transformers to 1,000 Layers》 则沿着这个思路进行尺度分析，根据分析结果调整了模型的归一化和初始化方案，最终成功训练出了 1000 层的 Transformer 模型。整个分析过程颇有参考价值，我们不妨来学习一下。

《DeepNet: Scaling Transformers to 1,000 Layers》

• URL：https://arxiv.org/abs/2203.00555

• Official Code：https://github.com/microsoft/torchscale

• 单位：微软亚洲研究院

DeepNet 理论分析

1）增量爆炸

这里的 “增量” 本质上指的是模型每一步的更新量，”爆炸” 表示更新量太大导致更容易陷入局部最优点（这与 “梯度爆炸” 的 “爆炸” 含义一致）

假设损失函数为 \(\mathcal{L}(\boldsymbol{\theta})\)，\(θ\) 是它的参数，考虑参数由 \(θ\) 变为 \(θ+Δθ\) 时损失函数的增量：

其中，\(\langle \cdot \rangle\) 表示链式法则相乘。

对于 SGD 有 \(\Delta\boldsymbol{\theta}=-\eta \nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})\)，那么 \(\Delta\mathcal{L} \approx -\eta\Vert\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})\Vert^2\)。

假设模型有 \(N\) 层，每层的平均参数量为 \(K\) 个，配合 Xavier 初始化以及各种 Normalization 手段，我们可以使得多数参数的梯度是 \(\mathscr{O}(1)\) 量级，所以有：

一个 \(n\) 维向量的模长平方公式为

\[\Vert\boldsymbol{x}\Vert^2 = \sum\limits_{i=1}^n x_i^2\]

显然这个公式是 \(n\) 项求和，因此显然就是 \(\mathscr{O}(n)\) 量级

因此，模型每一步的更新量 \(\Delta\mathcal{L}\) 是正比于模型深度 \(N\) 的（模型宽度 \(K\) 不在本文讨论范围）。如果模型层数越深，那么模型的更新量就越大，这意味着初始阶段模型 越容易进入不大好的局部最优点，然后训练停滞甚至崩溃，这就是 “增量爆炸” 问题。

这时候有两种解决方法：

• Warmup：初始阶段用更小的学习率 \(\eta\) 进行训练（不超过 \(η/N\) 量级），然后再慢慢增大学习率

• 调整初始化方案：使得模型参数的梯度 \(\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})\) 是 \(\mathscr{O}(1/\sqrt{N})\) 量级，这样最终模型每一步的更新量就是 \(\mathscr{O}(\eta K)\) 量级，自动抵消掉模型深度的影响

2）量级分析

怎么做到第二种方案呢？我们可以尝试分析 Transformer 的梯度。然而，精确的梯度求起来比较繁琐，并且事实上我们也 不需要精确的梯度，而只是要对梯度做一个量级分析，所以我们可以用如下的 “量级分解” 技巧转化为标量的导数问题。

对于一个矩阵 \(\boldsymbol{W}\)，我们将其分解为 \(\color{blue}{\boldsymbol{W}=\lambda \boldsymbol{U}}\) 的形式，其中

说白了，我们就是要将一个矩阵分解为一个标量 \(λ\) 与一个尽可能正交的矩阵 \(\boldsymbol{U}\) 之积。

由于 \(\boldsymbol{U}\) 接近正交矩阵，它起到了一个标准参考系的作用，而对应的 \(λ\) 则代表了矩阵 \(\boldsymbol{W}\) 的量级。如果 \(\boldsymbol{W}\) 使用 Xavier 初始化，那么 \(λ\) 相当于其中的 gain 参数，即在 Xavier 初始化的基础上还要再乘一个 \(λ\)。

当 \(\boldsymbol{W}=\lambda \boldsymbol{U}\) 且 \(\boldsymbol{U}\) 尽可能正交时，\(\Vert \boldsymbol{W}\boldsymbol{x}\Vert = \Vert \lambda\boldsymbol{U} \boldsymbol{x}\Vert=\lambda\Vert \boldsymbol{U} \boldsymbol{x}\Vert\approx\lambda\Vert \boldsymbol{x}\Vert\)，也就是说 \(\boldsymbol{W}\) 对向量模长的改变倍数大致上等于 \(λ\) ，而本文主要也是关心这个倍数，所以用这个倍数作为矩阵量级

这是因为 Xavier 初始化的结果就 接近一个正交矩阵，这一点可以参考 《从几何视角来理解模型参数的初始化策略》。

使用上述矩阵分解方法，我们有：

这意味着 \(\frac{∂L}{∂λ}\) 跟 \(\frac{∂L}{∂W}\) 在量级上是成正比的，所以对 \(\frac{∂L}{∂λ}\) 做量级分析就相当于对 \(\frac{∂L}{∂W}\) 做量级分析。这样 \(\frac{∂L}{∂λ}\) 就相当于 \(\frac{∂L}{∂W}\) 量级的一个简单的 “探针”，原来的矩阵求导就可以转化为标量求导，降低了分析难度。

3）FFN 层梯度

很多实验结果都显示虽然 Pre Norm 比 Post Norm 更容易训练，但 Post Norm 的最终效果往往更好些，所以原论文保留了 Post Norm 结构，并考虑了更一般的形式（DeepNorm）：

其中 \(\alpha > 0\) 是一个常数。

简单起见，我们首先考虑 Transformer 中的 FFN 层，有：

其中，\(\phi\) 是激活函数，一般为 ReLU 或其变体（Swish、GeLU 等），它们（近似）满足 \(\phi(\lambda x) = \lambda \phi(x),\forall \lambda > 0\)。

使用上一节的量级分解探针，可以得到：

求 \(\lambda_1\) 和 \(\lambda_2\) 的梯度，分别有：

这里，我们断言 \(\frac{\partial \mathcal{L}}{\partial \boldsymbol{x}_{l+1}}\)、\(\frac{\partial \boldsymbol{x}_{l+1}}{\partial \boldsymbol{z}_{l+1}}\) 都是 \(\mathscr{O}(1)\) 量级的，并且由于 \(\boldsymbol{U}_1\)、\(\boldsymbol{U}_2\) 都接近正交矩阵，所以 \(\phi(\boldsymbol{x}_l \boldsymbol{U}_1)\boldsymbol{U}_2\) 也是 \(\mathscr{O}(1)\) 量级的。最终有：

4）Self-Attention 梯度

现在考虑自 Self Attention，作为量级分析，我们考虑 单头注意力 即可，其形式为：

其中 \(\sigma(\cdot)\) 是 softmax 操作的简写，这里省略了 Attention 的 scale 操作。

对上式进行量级分解后的形式为：

现在我们可以对各个 \(λ\) 分别求梯度，而由于 softmax 的存在，事实上 \(λ_q\)、\(λ_k\) 的梯度本身会很小，不会明显影响最终的更新量，所以其实我们考虑 \(λ_v\)、\(λ_o\) 的更新量足矣：

同样的，我们断言 \(\frac{\partial \mathcal{L}}{\partial \boldsymbol{x}_{l+1}}\)、\(\frac{\partial \boldsymbol{x}_{l+1}}{\partial \boldsymbol{z}_{l+1}}\) 都是 \(\mathscr{O}(1)\) 量级的。

同时，由于 softmax 出来的是一个概率分布，然后对 \(x_l\) 的各个 token 做 加权平均，通常而言，平均前后的向量会在同一数量级，所以我们认为 \(\sigma (\lambda_q\lambda_k\boldsymbol{x}_l \boldsymbol{U}_q\boldsymbol{U}_k^{\top}\boldsymbol{x}_l^{\top})\boldsymbol{x}_l\boldsymbol{U}_v\boldsymbol{U}_o\) 也是 \(\mathscr{O}(1)\) 量级的。

因此，Self-Attention 的梯度与 FFN 的梯度类似，有：

5）初步结论

现在不管是 FFN 还是 Self Attention，我们都得到了相似的结论，现在简单起见，假设每个参数的量级（至少在初始化阶段）是一致的，即所有的 \(λ\) 取同一个值，那么总的结论是：

即梯度的量级是 \(\mathscr{O}(\lambda/\alpha)\)。

另一方面，我们说 \(N\) 层的 Transformer 模型，一般是 \(N\) 层的 Self Attention 加 \(N\) 层的 FFN，所以 严格来说层数是 \(2N\)。因此，按照 “增量爆炸” 一节的分析，我们需要将梯度调整到 \(\mathscr{O}(1/\sqrt{2N})\) 量级，上式告诉我们可以通过让 \(\color{blue}{\lambda/\alpha=1/\sqrt{2N}}\) 来实现。

原论文的放缩更为宽松一些，得到的结果是 \(\color{blue}{\lambda/\alpha = 1/\sqrt{4N}}\)，量级上是等价的。

现在我们得到了 \(λ\) 与 \(α\) 的一个比例关系，但无法直接得到 \(λ\) 和 \(α\) 的具体值。按照论文的说法，是从对称角度出发，让 \(\color{blue}{λ=1/α}\)，从而可以解得：

然而，单纯对称的解释显然是不够说服力的，我们需要搞清楚不同的选择究竟有什么不同的结果。为此，我们可以比较另外两组解：

另解一：\(\alpha=1,\lambda=(2N)^{-1/2}\)

• 此时 参数的初始化缩小到原来的 \((2N)^{−1/2}\) 倍，梯度也被缩小到原来的 \((2N)−1/2\) 倍，根据 SGD 的 \(\Delta\boldsymbol{\theta}=-\eta \nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})\) 得出每步的更新量也是原来的 \((2N)^{−1/2}\) 倍，

• 也就是说，调整前后的相对学习幅度是没有变化的，因此有可能刚开始 \(λ=\mathscr{O}((2N)^{−1/2})\) 级别，但训练集几步后就脱离了这个量级了。

另解二：\(\alpha=(2N)^{1/2},\lambda=1\)

• 此时 参数的初始化没有缩小，但梯度也被缩小到原来的 \((2N)^{−1/2}\) 倍，根据 SGD 的 \(\Delta\boldsymbol{\theta}=-\eta \nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})\) 得出每步的更新量也是原来的 \((2N)^{−1/2}\) 倍

• 调整前后的相对学习幅度是明显缩小了，因此有可能出现学习得非常慢的情况。

这里的 \(\alpha\) 负责对梯度进行放缩，而 \(\lambda\) 负责对参数的初始化进行放缩

这两种情况看上去都各有缺点，因此介乎两者之间的

似乎就能解释得通了。它就是 保持梯度缩放 到原来的 \((2N)^{-1/2}\) 倍的同时， 让初始学习步伐稍微慢一些，但又不至于太慢，隐式地起到了 Warmup 的作用。

6）多种优化器

上面的分析都是基于 SGD 优化器进行的，但事实上我们很少直接用 SGD 去训练 NLP 模型，我们更多是自适应学习率优化器，主要有两大类：

• 一类是用二阶矩来校正学习率， Adam、AdamW 等都属此类；

• 另一类是通过参数模长进一步校正学习率，比如 LAMB、AdaFactor。

原论文的说法是 “我们在 SGD 上进行推导，然后在 Adam 上验证发现也还可以”，但从理论上来讲，它们并不完全通用，这一节我们就来针对性地做一下分析。

对于 Adam 类优化器，每一步的参数更新量大约是 \(\Delta\boldsymbol{\theta}=-\eta\,\text{sign}(\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}))\)，所以模型的更新量 \(\Delta\mathcal{L} \approx -\eta\Vert\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})\Vert_1\)，是正比于梯度的 1 次方而不是 2 次方。

这里的 \(\text{sign}\) 是指示函数

因此，如果想使得模型的更新量跟层无关，那么梯度应该缩小为原来的 \(1/(2N)\)，即应该有 \(\lambda/\alpha=1/(2N)\)。

如果同样让 \(\lambda=1/\alpha\)，那么有：

对于 LAMB 类优化器，每一步的参数更新量大约是 \(\Delta\boldsymbol{\theta}=-\eta\Vert\theta\Vert\,\text{sign}(\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}))\)，所以模型的更新量为 \(\Delta\mathcal{L} \approx -\eta\Vert\theta\Vert\Vert\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})\Vert_1\)。

由于参数的缩放比例是 \(\lambda\)，梯度的缩放比例是 \(\lambda/\alpha\)，所以 \(\Delta\mathcal{L}=\mathscr{O}(2N\lambda^2/\alpha)\)，从而 \(\lambda^2/\alpha=1/(2N)\)。

这类优化器每一步的相对更新量是一样的（等于学习率 \(\eta\)），不管怎么调整 \(\alpha\)、\(\lambda\)，其相对更新大小都不会变化，所以我们直接取 \(\alpha=1,\lambda=(2N)^{-1/2}\)。

各种优化器的结果对比如下所示：

7）事后分析

前面的两节推导过程都用到了断言 ”\(\frac{∂L}{∂x_{l+1}}\)、\(\frac{∂x_{l+1}}{∂z_{l+1}}\) 都是 \(\mathscr{O}(1)\)的”，那么它是否成立呢？这里我们事后分析一下。

其实也很简单，

• 经过前述调整后，不管是 FFN 层还是 Self Attention 层，初始阶段每个残差分支的权重被缩放到原来的 \(λ^2/α\) 倍

• 不管是哪种优化器的结果，\(λ^2/α\) 都是一个比较小的数字，这意味着初始阶段整个模型其实 接近一个恒等函数

因此 \(\frac{∂L}{∂x_{l+1}}\)、\(\frac{∂x_{l+1}}{∂z_{l+1}}\) 自然都是 \(\mathscr{O}(1)\) 的，所以结论和断言是自洽的。

另外，可能有读者想问同样的分析是否可以用到 Pre Norm 结构 上呢？答案是可以的，并且结论是基本一致的，只是因为 Norm 放在了残差分支之前，所以就没必要设置 $$α$$ 参数了。

因此，结论就是：上述关于 Post Norm 的结果中所有的 \(α\) 都等于为 \(1\)，然后重新计算相应的 \(λ\)。

最后，读者可能有疑问的是花了那么多功夫讨论把模型做深，那么模型深度真有那么重要吗？有，原论文给出了一个漂亮的实验结果，用一个 200 层的 “深而窄” 的模型（32 亿参数），战胜了之前 48 层 “浅而宽” 的 SOTA 模型（120 亿参数）：

DeepNet 代码

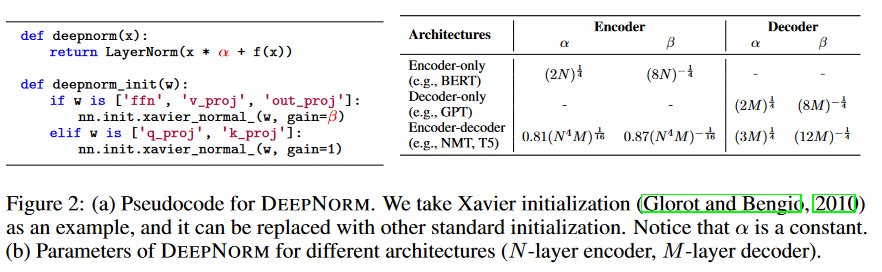
DeepNet 的伪代码如下图所示：

参考

• DeepNet 论文：DeepNet: Scaling Transformers to 1,000 Layers

• 苏剑林博客：训练1000层的Transformer究竟有什么困难？