为什么现在的 LLM 都是 Decoder-only 架构？

本文主要参考了为什么现在的LLM都是Decoder-only的架构？、《为什么现在的LLM都是Decoder-only的架构？》FAQ 和知乎问题《为什么现在的LLM都是Decoder only的架构？》，侵删。

0、LLM

LLM 是 “Large Language Model” 的简写，目前一般指 百亿参数以上 的语言模型，主要面向文本生成任务。跟小尺度模型（10 亿或以内量级）的 “百花齐放” 不同，目前 LLM 的一个现状是 Decoder-only 架构的研究居多，像 OpenAI 一直坚持 Decoder-only 的 GPT 系列就不说了，即便是 Google 这样的并非全部押注在 Decoder-only 的公司，也确实投入了不少的精力去研究 Decoder-only 的模型，如 PaLM 就是其中之一。那么，为什么 Decoder-only 架构会成为 LLM 的主流选择呢？

知乎上也有同款问题《为什么现在的LLM都是Decoder only的架构？》，上面的回答大多数聚焦于 Decoder-only 在 训练效率和工程实现上的优势，那么它有没有 理论上的优势 呢？本文试图从这个角度进行简单的分析。

匹配任务和定位任务

匹配任务：CLS Token
定位任务：Localization Regression

无法直接迁移

全量微调预训练模型比较困难

L_match 用于判断查询 Q 是否与视频 V 相关，从而进行跨模态语义对齐。具体来说，CLS Token 用来计算匹配分数（matching score），通过一个 Linear Layer（\sigma(\cdot)）实现。为了提高模型的学习效率（Learning Efficiency），作者采用了 triplet loss：

如果学习率 (LR) 太小，就会发生过拟合。大的学习率有助于规范训练，但如果学习率太大，训练就会发散。因此，可以通过短期网格搜索来找到收敛或发散的学习率，但有一种更简单的方法：Cyclical Learning Rates（CLR）以及 Learning Rate Range Test（LR range test）。 CLR’s simplest way -> Learning Rate Change Linear

Weight Decay

If you have no idea of a reasonable value for weight decay, test 10−3 , 10−4 , 10−5 , and 0.

Smaller datasets and architectures seem to require larger values for weight decay while larger datasets and deeper architectures seem to require smaller values.

Our hypothesis is that complex data provides its own regularization and other regularization should be reduced.

对于较大的数据集，可以使用较小的 Weight Decay；反之则需要设置较大的 weight decay；
对于较大的 LR，需要设置较小的 Weight Decay；反之则需要较大的 weight decay； Reducing other forms of regularization and regularizing with very large learning rates makes training significantly more efficient.

Weight Decay 比较合理的值：1e-3、5e-4（尽量在 1e-3 到 1e-5 的区间内，但不知道模型复杂度和数据集大小时，最保守的是从 1e -4 周围开始尝试）

Momentum

However, if a constant learning rate is used then a large constant momentum (i.e., 0.9-0.99) will act like a pseudo increasing learning rate and will speed up the training.

【1712579】 BS = 256 Adam Optimizer find_lr （find_lr.log）

Trick：gumbel_softmax

import torch
import torch.nn.functional as F

# logits: (BS, 128)
# gumbel: (BS, 128) -> (BS, 128, 1)
gumbel = F.gumbel_softmax(logits, tau=1, hard=True).unsqueeze(-1)

1、统一视角

需要指出的是，笔者目前训练过的模型，最大也就是 10 亿级别的，所以从 LLM 的一般概念来看是没资格回答这个问题的，下面的内容只是笔者根据一些研究经验，从偏理论的角度强行回答一波。文章多数推论以自己的实验结果为引，某些地方可能会跟某些文献的结果冲突，请读者自行取舍。

我们知道，一般的 NLP 任务都是根据给定的输入来预测输出，完全无条件的随机生成是很少的，换句话说，任何 NLP 任务都可以分解为 “输入” 跟 “输出” 两部分，我们可以把处理 “输入” 的模型叫做 Encoder，生成 “输出” 的模型叫做 Decoder，那么所有任务都可以从 “Encoder-Decoder” 的视角来理解，而不同模型之间的差距在于 Encoder、Decoder 的注意力模式以及是否共享参数，如下所示：

\[\begin{array}{c|ccc} \hline & \text{Encoder 注意力} & \text{Decoder 注意力} & \text{是否共享参数} \\ \hline \text{GPT} & \text{单向} & \text{单向} & \text{是} \\ \text{UniLM} & \text{双向} & \text{单向} & \text{是} \\ \text{T5} & \text{双向} & \text{单向} & \text{否} \\ \hline \end{array}\]

这里，

GPT 就是 Decoder-only 的代表作；
UniLM 则是跟 GPT 相似的 Decoder 架构，但它是混合的注意力模式；
T5 则是 Encoder-Decoder 架构的代表作，主要是 Google 比较感兴趣；

Google 在 T5 和 UL2 两篇论文中做了较为充分的对比实验，结果均体现出了 Encoder-Decoder 架构相比于 Decoder-only 的优势，但由于从 LLM 的角度看 这两篇论文的模型尺度都还不算大，以及多数的 LLM 确实都是在做 Decoder-only 的，所以这个优势能否延续到更大尺度的 LLM 以及这个优势本身的缘由，依然都还没有答案。

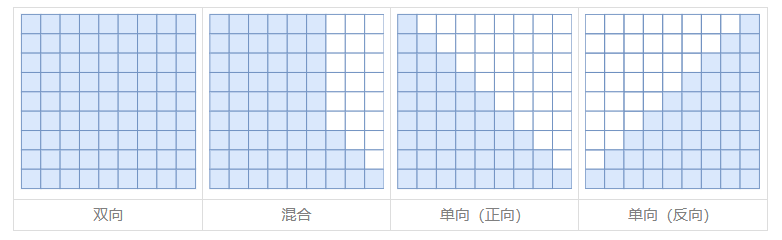
LLM 中的四种注意力

其中，

双向 attention 也称为 full attention
混合 attention 也称为 mixture attention
单向 attention 也称为 casual attention
- 也就是有方向（单向）的 attention，是从因到果的方向

几种经典的 pre-trained LM

图片来源：Pre-train, Prompt, and Predict: A Systematic Survey of Prompting Methods in Natural Language Processing

2、对比实验

从上表可以看出，其实 GPT 跟 UniLM 相比才算是严格控制变量的，如果 GPT 直接跟 T5 相比，那实际上产生了两个变量：输入部分的注意力改为双向以及参数翻了一倍。而之所以会将它们三个一起对比，是因为它们的推理成本大致是相同的。

相比 GPT，既然 T5 有两个变量，那么我们就无法确定刚才说的 Encoder-Decoder 架构的优势，究竟是输入部分改为双向注意力导致的，还是参数翻倍导致的。为此，笔者在10亿参数规模的模型上做了 GPT 和 UniLM 的对比实验，结果显示对于同样输入输出进行从零训练（Loss 都是只对输出部分算，唯一的区别就是输入部分的注意力模式不同），UniLM 相比 GPT 并无任何优势，甚至某些任务更差。

假设这个结论具有代表性，那么我们就可以初步得到结论：

输入部分的注意力改为双向不会带来收益，Encoder-Decoder 架构的优势很可能只是源于参数翻倍。

换句话说，在同等参数量、同等推理成本下，Decoder-only 架构很可能是最优选择。当然，要充分验证这个猜测，还需要补做一些实验，比如 Encoder 和 Decoder 依然不共享参数，但 Encoder 也改为单向注意力，或者改为下一节介绍的正反向混合注意力，然后再对比常规的 Encoder-Decoder 架构。但笔者的算力有限，这些实验就留给有兴趣的读者了。

3、低秩问题

为什么 “输入部分的注意力改为双向不会带来收益” 呢？明明输入部分不需要考虑自回归生成，直觉上应该完整的注意力矩阵更好呀？笔者猜测，这很可能是因为 双向注意力的低秩问题 带来的效果下降。

众所周知，（完整的）Attention 矩阵一般是由一个 低秩分解的矩阵 加 softmax 而来，具体来说是一个 \(n\times d\) 的矩阵与 \(d\times n\) 的矩阵相乘后再加 softmax（\(n \gg d\)），softmax 的范围 \((0, 1)\)，这种形式的 Attention 的矩阵 因为低秩问题而带来表达能力的下降，具体分析可以参考《Attention is Not All You Need: Pure Attention Loses Rank Doubly Exponentially with Depth》。

其中，\(n\) 是序列长度；\(d\) 是 head_size，而不是 hidden_size。在多头注意力中，\(\text{head_size} = \text{hidden_size} / \text{heads}\)。
对于 BERT base，\(\text{head_size} = 768 / 12 = 64\)，而预训练长度 \(n\) 一般是 512，所以 \(n \gg d\) 大致上是成立的。

而 Decoder-only 架构的 Attention 矩阵是一个 下三角阵，注意三角阵的行列式等于它对角线元素之积，由于 softmax 的存在，对角线必然都是正数，所以它的行列式必然是正数，即 Decoder-only 架构的 Attention 矩阵一定是满秩的！满秩意味着 理论上有更强的表达能力，也就是说，Decoder-only 架构的 Attention 矩阵在理论上具有更强的表达能力，改为双向注意力反而会变得不足。

低秩：行列式值为 0，线性相关（有冗余的相关信息）
表达能力下降
满秩：行列式值不为 0，线性无关
有更强的表达能力

还有个间接支持这一观点的现象，那就是线性 Attention 在语言模型任务 (Language Modeling) 上（单向注意力）与标准 Attention 的差距，小于它在 MLM (Masked Language Modeling) 任务上（双向注意力）与标准 Attention 的差距，也就是说，线性 Attention 在双向注意力任务上的效果相对更差。这是因为：

线性 Attention 在做语言模型任务时，它的 Attention 矩阵跟标准 Attention 一样都是满秩的下三角阵；
在做 MLM 任务时，线性 Attention 矩阵的秩比标准 Attention 矩阵更低；

线性 Attention 是 \(n\times d\) 的矩阵与 \(d\times n\) 的矩阵相乘，秩一定不超过 \(d\)；
标准 Attention 是 \(n\times d\) 的矩阵与 \(d\times n\) 的矩阵相乘后加 softmax；
softmax 会有一定的升秩作用，参考《Transformer升级之路：3、从Performer到线性Attention》中的 “低秩问题”一节及评论区

反过来，这个结论能不能用来 改进像 BERT 这样的双向注意力模型 呢？思路并不难想，比如：

在 Multi-Head Attention 中，一半 Head 的 Attention 矩阵截断为下三角阵（正向注意力），另一半 Head 的 Attention 矩阵截断为上三角阵（反向注意力）；
奇数层的 Attention 矩阵截断为下三角阵（正向注意力），偶数层的 Attention 矩阵截断为上三角阵（反向注意力）。

这两种设计都可以既保持模型整体交互的双向性（而不是像 GPT 一样，前一个 token 无法跟后一个 token 交互），又融合 单向注意力的满秩优点。

苏剑林也简单做了对比实验，发现正反向混合的注意力在 MLM 任务上是比像 BERT 这样的全双向注意力模型效果稍微要好点的，如下图所示：

全双向注意力与正反向混合注意力的训练曲线比较

好消息是看得出略有优势，间接支持了前面的猜测；
坏消息是这实验的只是一个 base 版本（1 亿参数）的模型，更大模型的效果尚未清楚。

总结

本文对 GPT 和 UniLM 两种架构做了对比实验，然后结合以往的研究经历，猜测了如下结论：

输入部分的注意力改为双向不会带来收益，Encoder-Decoder 架构的优势很可能只是源于 参数翻倍（多了一倍的参数）；
Encoder 的双向注意力没有带来收益，可能是因为 双向注意力的低秩问题 导致效果下降；

所以，基于这两点推测，我们得到结论：

在 同等参数量、同等推理成本 下，Decoder-only 架构是最优选择。

解答

“双向注意力的低秩问题带来的效果下降” 这看起来像一个 bug。现在工业界绝大多数模型都是双向注意力，波及范围也太广了吧？

答：我们并没有说 “双向注意力在任何任务上都非常糟糕” 之类的结论，”现在工业界绝大多数模型都是双向注意力” 这个现象其实跟原文的结论并不冲突。我们在原文的实验结论是 “在生成任务上的 Encoder 引入双向注意力似乎不会带来收益”，结论的条件是很明确的——”在生成任务的 Encoder”。

会不会还有一个原因，下三角或上三角 mask 更能够 把位置编码的信息处理得更好？

答：这确实是一个 很新颖的观点，我没有从这个角度思考过。但事实上，三角形 mask 除了带来秩的提升外，确确实实也带来了位置识别上的优势，它打破了 transformer 的置换不变性，直接引入了从左往右的序，所以甚至不加位置编码都行。也许两者都是起作用的原因。

综述
- Decoder-Only or Encoder-Decoder? Interpreting Language Model as a Regularized Encoder-Decoder

参考

苏剑林：
- 为什么现在的LLM都是Decoder-only的架构？
- 《为什么现在的LLM都是Decoder-only的架构？》FAQ
知乎问题：为什么现在的LLM都是Decoder only的架构？

文档信息

本文作者：Bookstall
本文链接：https://bookstall.github.io/2023/04/03/why-now-LLM-is-decoder-only/
版权声明：自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）

Bookstall