积分梯度（Integrated Gradients）

前言

本文介绍一种神经网络的可视化方法：积分梯度（Integrated Gradients），它首先在论文《Gradients of Counterfactuals》中提出，后来《Axiomatic Attribution for Deep Networks》再次介绍了它，两篇论文作者都是一样的（都是 Google 的工作），内容也大体上相同，后一篇相对来说更易懂一些，如果要读原论文的话，建议大家优先读后一篇。当然，它已经是 2016～2017 年间的工作了，”新颖” 说的是它思路上的创新有趣，而不是指最近发表。

所谓可视化，简单来说就是对于给定的输入 $x$ 以及模型 $F(x)$，我们想办法指出 $x$ 的哪些分量对模型的决策有重要影响，或者说对 $x$ 各个分量的重要性做个排序，用专业的话术来说那就是 “归因”。一个朴素的思路是直接使用梯度 $∇xF(x)$ 来作为 $x$ 各个分量的重要性指标，而积分梯度是对它的改进。然而，很多介绍积分梯度方法的文章（包括原论文），都过于 “生硬”（形式化），没有很好地突出 积分梯度 能比 朴素梯度 更有效的本质原因。本文试图用自己的思路介绍一下积分梯度方法。

朴素梯度

首先，我们来学习一下基于梯度的方法，其实它就是基于 泰勒展开：

\[\begin{equation} F(x+\Delta x) - F(x) \approx \langle\nabla_x F(x), \Delta x\rangle=\sum_i [\nabla_x F(x)]_i \Delta x_i\label{eq:g} \end{equation}\]

我们知道 $∇xF(x)$ 是大小跟 $x$ 一样的向量，这里 $[∇xF(x)]_i$ 为它的第 $i$ 个分量，那么对于同样大小的 $Δxi$ ，$[∇xF(x)]_i$ 的 绝对值越大，那么 $F(x+Δx)$ 相对于 $F(x)$ 的变化就越大，也就是说：

$[∇xF(x)]_i$ 衡量了模型对输入的第 $i$ 个分量的 敏感程度，所以我们用 $\|[∇xF(x)]_i\|$ 作为第 $i$ 个分量的重要性指标。

这种思路比较简单直接，在论文《How to Explain Individual Classification Decisions》和《Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps》都有描述，在很多时候它确实也可以成功解释一些预测结果，但它也有明显的缺点。很多文章提到了饱和区的情况，也就是一旦进入到了 饱和区（典型的就是 ReLU 的负半轴），梯度就为 $0$ 了，那就揭示不出什么有效信息了。

从实践角度看，这种理解是合理的，但是笔者认为还不够深刻。从苏神之前的文章《对抗训练浅谈：意义、方法和思考（附Keras实现）》可以看出，对抗训练的目标可以理解为就是在推动着 $∥∇xF(x)∥2→0$，这也就可以理解为，梯度是可以被 "操控" 的，哪怕不影响模型的预测准确率的情况下，我们都可以让梯度尽可能接近于 $$0$$。所以，回到本文的主题，那就是：$[∇xF(x)]_i$ 确实衡量了模型对输入的第 $i$ 个分量的敏感程度，但敏感程度不足以作为重要性的良好度量。

Integrated Gradients（IG）

鉴于直接使用梯度的上述缺点，一些新的改进相继被提出来，如 LRP、DeepLift 等，不过相对而言，笔者还是觉得 积分梯度 的改进 更为简洁漂亮。

参照物

首先，我们需要换个角度来理解原始问题：我们的目的是找出比较重要的分量，但是这个重要性不应该是绝对的，而应该是相对的。比如，我们要找出近来比较热门的流行词，我们就不能单根据词频来找，不然找出来肯定是 “的”、”了” 之类的停用词，我们应当准备一个平衡语料统计出来的 “参照” 词频表，然后对比词频差异而不是绝对值。这就告诉我们，为了衡量 $x$ 各个分量的重要性，我们也需要有一个 “参照物” $\bar{x}$。

当然，很多场景下我们可以简单地让 $\bar{x}=0$，但这未必是最优的，比如我们还可以选择 $\bar{x}$ 为所有训练样本的均值。我们期望 $F(\bar{x})$ 应当给一个比较平凡的预测结果，比如分类模型的话，$\bar{x}$ 的预测结果应该是每个类的概率都很均衡。于是我们去考虑 $F(\bar{x})−F(x)$ ，我们可以想象为这是 从 $x$ 移动到 $\bar{x}$ 的成本。

如果还是用近似展开 (1)，那么我们将得到：

\[\begin{equation} F(\bar{x})-F(x) \approx \sum_i [\nabla_x F(x)]_i [\bar{x} - x]_i\label{eq:g2} \end{equation}\]

对于上式，我们就可以有一种新的理解：

从 $x$ 移动到 $\bar{x}$ 的 总成本 为 $F(\bar{x})−F(x)$ ，它是每个分量的成本之和，而每个分量的成本近似为 $[∇_xF(x)]_i[\bar{x}−x]_i$ ，所以我们可以用 $\|[∇xF(x)]_i[\bar{x}−x]_i\|$ 作为第 $i$ 个分量的重要性指标。

成本越大，说明第 $i$ 个分量对结果的影响更大，也就更重要。

当然，不管是 $[∇_xF(x)]_i$ 还是 $\|[∇_xF(x)]_i[\bar{x}−x]_i\|$，它们的缺陷在数学上都是一样的（梯度消失），但是对应的解释却并不一样。前面说了，$[∇_xF(x)]_i$ 的缺陷源于 “敏感程度不足以作为重要性的良好度量”，而纵观这一小节的推理过程，$\|[∇_xF(x)]_i[\bar{x}−x]_i\|$ 的缺陷则只是因为 “等式(2)仅仅是近似成立的”，但整个逻辑推理是没毛病的。

积分恒等

很多时候一种新的解释能带给我们新的视角，继而启发我们做出新的改进。比如前面对缺陷的分析，说白了就是说 “$\|[∇_xF(x)]_i[\bar{x}−x]_i\|$ 不够好是因为式(2)不够精确”，那如果我们直接能找到一个精确相等的类似表达式，那么就可以解决这个问题了。

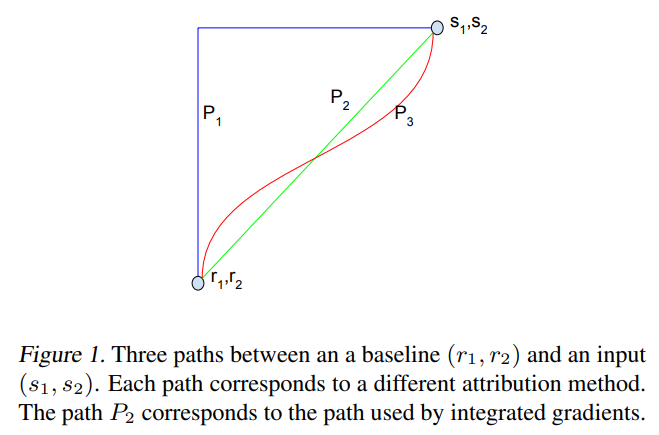
integrated gradients

积分梯度正是找到了这样的一个表达式：设 $γ(α),α\in[0,1]$ 代表连接 $x$ 和 $\bar{x}$ 的一条 参数曲线，其中 $γ(0)=x,γ(1)=\bar{x}$，那么我们有：

\[\begin{equation} \begin{aligned} F(\bar{x})-F(x) =&\, F(\gamma(1))-F(\gamma(0))\\ =& \int_0^1 \frac{dF(\gamma(\alpha))}{d\alpha}d\alpha\\ =& \int_0^1 \left\langle\nabla_{\gamma} F(\gamma(\alpha)), \gamma'(\alpha)\right\rangle d\alpha\\ =& \sum_i \int_0^1 \left[\nabla_{\gamma} F(\gamma(\alpha))\right]_i \left[\gamma'(\alpha)\right]_i d\alpha \end{aligned} \label{eq:g3} \end{equation}\]

可以看到，式(3)具有跟(2)一样的形式，只不过将 $[∇_xF(x)]_i[\bar{x}−x]_i$ 换成了 $∫10[∇_γF(γ(α))]i[γ′(α)]idα$。但式(3)是精确的积分恒等式，所以积分梯度就提出使用

\[\begin{equation} \left|\int_0^1 \left[\nabla_{\gamma} F(\gamma(\alpha))\right]_i \left[\gamma'(\alpha)\right]_i d\alpha\right|\label{eq:ig-1} \end{equation}\]

作为第 $i$ 个分量的重要性度量。

最简单的方案自然就是：将 $\gamma{\alpha}$ 取为两点间的直线，即：

\[\begin{equation} \gamma(\alpha) = (1 - \alpha) x + \alpha \bar{x} \end{equation}\]

这时候积分梯度具体化为：

\[\begin{equation} \left|\left[\int_0^1 \nabla_{\gamma} F(\gamma(\alpha))\big|_{\gamma(\alpha) = (1 - \alpha) x + \alpha \bar{x}}d\alpha\right]_i \left[\bar{x}-x\right]_i\right|\label{eq:ig-2} \end{equation}\]

所以相比 $\|[∇_xF(x)]_i[\bar{x}−x]_i\|$ 的话，就是用梯度的积分 $∫10∇_γF(γ(α))\|γ(α)=(1−α)x+α\bar{x}dα$ 替换 $∇_xF(x)$ ，也就是从 $x$ 到 $\bar{x}$ 的直线上每一点的梯度的平均结果。直观来看，由于考虑了整条路径上的所有点的梯度，因此就不再受某一点梯度为 $0$ 的限制了。

如果读者看了积分梯度的两篇原始论文，就会发现原论文的介绍是反过来的：先莫名其妙地给出式 (6)，然后再证明它满足两点莫名其妙的性质（敏感性和不变性），接着证明它满足式 (3)。总之就是带着读者做了一大圈，就是没说清楚它是一个更好的重要性度量的本质原因——大家都是基于对 $F(\bar{x})−F(x)$ 的分解，而式 (3) 比式 (2) 更为精确。

离散近似

最后就是这个积分形式的量怎么算呢？深度学习框架没有算积分的功能呀。其实也简单，根据积分的 “近似-取极限” 定义，我们直接用 离散近似 就好，以式 (6) 为例，它近似于：

\[\begin{equation} \left\|\left[\frac{1}{n}\sum_{k=1}^n\Big(\nabla_{\gamma} F(\gamma(\alpha))\big|_{\gamma(\alpha) = (1 - \alpha) x + \alpha \bar{x}, \alpha=k/n}\Big)\right]_i \left[\bar{x}-x\right]_i\right\| \end{equation}\]

所以还是那句话，本质上就是 “从 $x$ 到 $\bar{x}$ 的直线上每一点的梯度的平均”，比单点处的梯度效果更好。

实验

原始论文的实现：https://github.com/ankurtaly/Integrated-Gradients

下面是原论文的一些效果图：

原论文中对梯度和积分梯度的比较（CV任务，可以看到积分梯度能更精细地突出重点特征）

原论文中对梯度和积分梯度的比较（NLP任务，红色为正相关，蓝色是负相关，灰色为不相关）

PyTorch 代码

作为一种常用的可解释人工智能方法，IG 算法被广泛集成到了各种代码库中，比如 pytorch 官方的 explainable AI 仓库 Captum 中就提供了包括 IG 在内的多种可解释人工智能方法。

Captum 支持的算法

创建模型

import numpy as np

import torch
import torch.nn as nn

from captum.attr import (
    GradientShap,
    DeepLift,
    DeepLiftShap,
    IntegratedGradients,
    LayerConductance,
    NeuronConductance,
    NoiseTunnel,
)

class ToyModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.lin1 = nn.Linear(3, 3)
        self.relu = nn.ReLU()
        self.lin2 = nn.Linear(3, 2)

        # initialize weights and biases
        self.lin1.weight = nn.Parameter(torch.arange(-4.0, 5.0).view(3, 3))
        self.lin1.bias = nn.Parameter(torch.zeros(1,3))
        self.lin2.weight = nn.Parameter(torch.arange(-3.0, 3.0).view(2, 3))
        self.lin2.bias = nn.Parameter(torch.ones(1,2))

    def forward(self, input):
        return self.lin2(self.relu(self.lin1(input)))

使用 IG 算法：

model = ToyModel()
model.eval()

torch.manual_seed(123)
np.random.seed(123)

# batch_size = 2
input = torch.rand(2, 3) 
baseline = torch.zeros(2, 3) # Ground Truth

ig = IntegratedGradients(model)
attributions, delta = ig.attribute(
    input,
    baseline, 
    target=0, 
    return_convergence_delta=True
)
print('IG Attributions:', attributions) # IG 值
print('Convergence Delta:', delta) # 置信度
"""
IG Attributions: tensor([[-0.5922, -1.5497, -1.0067],
                         [ 0.0000, -0.2219, -5.1991]])
Convergence Delta: tensor([2.3842e-07, -4.7684e-07])
"""

参考

论文：Gradients of Counterfactuals
论文：Axiomatic Attribution for Deep Networks
苏剑林：积分梯度：一种新颖的神经网络可视化方法
工具：Captum

文档信息

本文作者：Bookstall
本文链接：https://bookstall.github.io/2023/03/16/integrated-gradient/
版权声明：自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）

Bookstall