SimCSE 通过简单的 “Dropout两次” 来构造 正样本 进行 对比学习，达到了无监督语义相似度任务的全面 SOTA。无独有偶，微软发布的论文《R-Drop: Regularized Dropout for Neural Networks》提出了 R-Drop，它将 “Dropout两次” 的思想用到了有监督任务中，每个实验结果几乎都取得了明显的提升。

R-Drop（Regularized Dropout）

《R-Drop: Regularized Dropout for Neural Networks》

• URL：https://arxiv.org/abs/2106.14448

• 单位：微软亚洲研究院

• 会议：NeurIPS 2021

• Official Code：https://github.com/dropreg/R-Drop

前言

1）Institution

Though simple and effective, there is a huge inconsistency between training and inference that hinders the model performance. That is, the training stage takes the sub model with randomly dropped units, while the inference phase adopts the full model without dropout. Also, the sub models caused by randomly sampled dropout units are also different without any constraints. Based on above observations and the randomness of the structure brought by dropout, we propose our R-Drop to regularize the output predictions of sub models from dropout.

一句话：训练阶段使用 Dropout 与推理阶段不使用 Dropout 之间存在 Gap，并且每个子模型是随机的、不受约束的。

2）结论

In this paper, we proposed a simple yet very effective consistency training method built upon dropout, namely R-Drop, which minimizes the bidirectional KL-divergence of the output distributions of any pair of sub models sampled from dropout in model training. Experimental results on 18 popular deep learning datasets show that not only can our R-Drop effectively enhance strong models, e.g., ViT, BART, Roberta-large, but also work well on large-scale datasets and even achieve SOTA performances when combined with vanilla Transformer on WMT14 English→German and English→French translations. Due to the limitation of computational resources, for pre-training related tasks, we only tested R-Drop on downstream task fine-tuning in this work. We will test it on pre-training in the future. In this work, we focused on Transformer based models. We will apply R-Drop to other network architectures such as convolutional neural networks.

整体结构

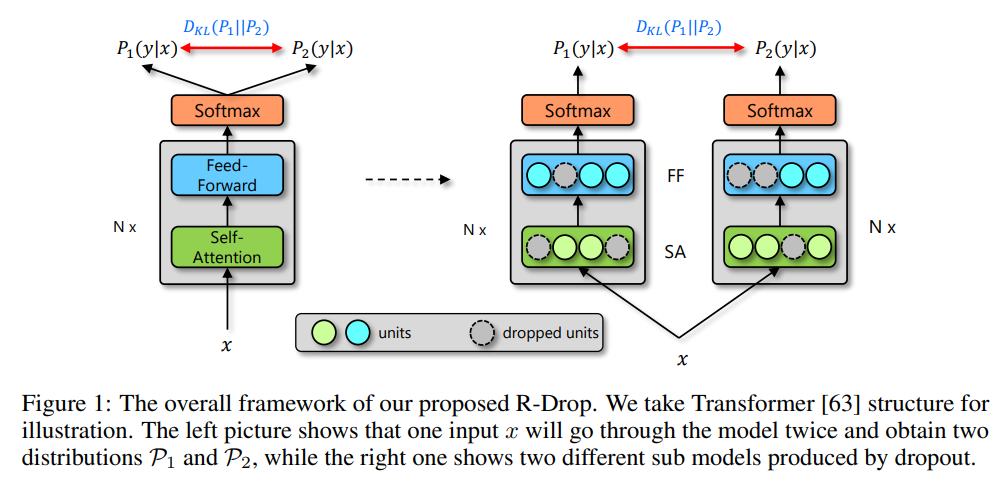
作者基于 Dropout 做了一个可推广的简单粗暴的优化方法。同样的输入，同样的模型，分别走过两个 Dropout 得到的将是两个不同的分布，近似将这两个路径网络看作两个不同的模型网络（Sub Network），如下图所示：

具体的公式表达如下图所示：

其中，超参数 \(\alpha\) 要根据不同的任务进行具体的设置。

KL-Divergence 的作用是希望不同 Dropout 的模型输出尽可能一致

训练过程

在训练过程中，为了节省训练时间，并不是将同一个输入输入两次，而是将输入句子复制一遍，然后拼接到一起，这样就相当于将 batch size 扩大了一倍，这个可以节省大量的训练时间，当然相比于原始的模型，这个会使得每个 step 的训练时间增加了，因为模型的训练复杂度提高了，所以需要更多的时间去收敛。训练如下：

作者在附录 B 中，通过数学证明，R-Drop 通过引入同一个样本，经过同一个模型的不同 Dropout，输出的概率要尽可能相等的优化目标，等价于令模型的所有参数尽可能相等的正则化约束，具体的证明可以看论文里面的推导。

实验

在 5 个任务（机器翻译任务、生成式摘要任务、NLU 任务、语言模型任务、图像分类任务），共 18 个数据集上都取得不俗的表现，从实验的结果来看，引入 R-Drop 都能给指标带来 1%~10% 的提升。

机器翻译任务：

‍‍‍‍‍‍‍‍‍‍‍‍‍自然语言理解任务：

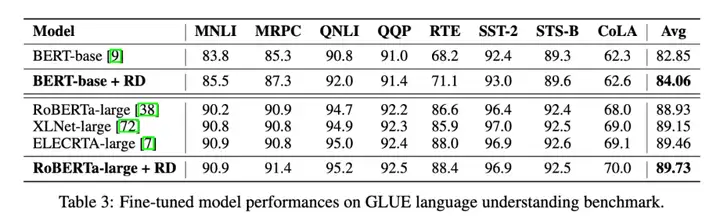
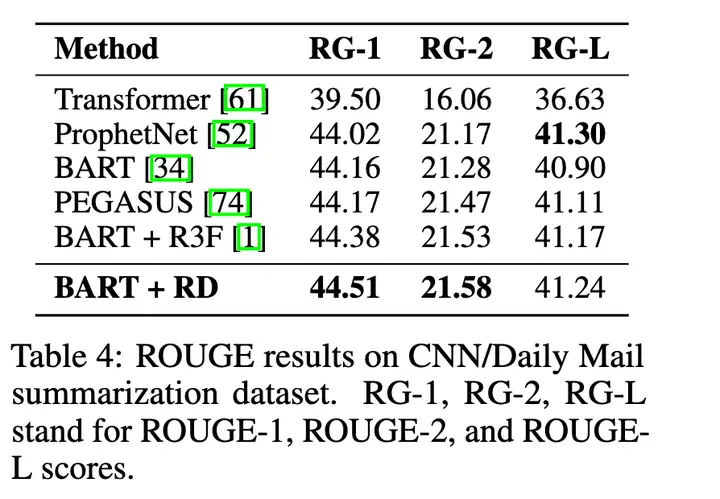
生成式摘要任务：

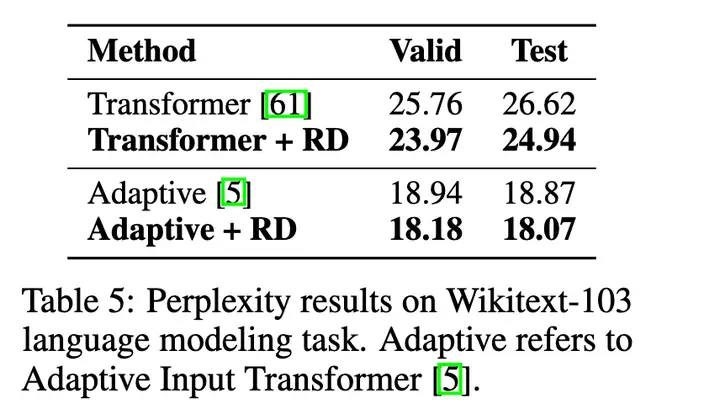
语言模型任务：

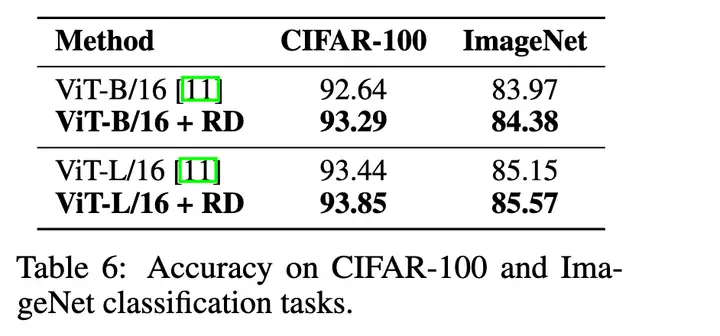
图像分类任务：

美团经验之谈

参考：R-Drop：提升有监督任务性能最简单的方法

本质上来说，R-Drop 与 MixUp、Manifold-MixUp 和 Adversarial Training（对抗训练）一样，都是一种数据增强方法，在小样本学习场景中用的非常多。小样本学习在美团点评业务上的 Benchmark 效果对比中，R-Drop 的结果也是优于其它三种数据增强方法。

Trick 探索

参考：R-Drop—-更强的正则化dropout

1）m-time R-Drop

同一个输入会输入两次，得到不同的结果，然后进行训练，但是 可不可以输入三次甚至更多次呢？论文实验了输入 3 次，发现和 2 次并没有什么太大区别，所以认为 2 次已经对模型有一个很强的正则化影响了。

2）Two Dropout Rates

对于两次同一个输入，dropout 的概率是一样的，那 不一样 效果会不会更好，实验结果如下图所示：

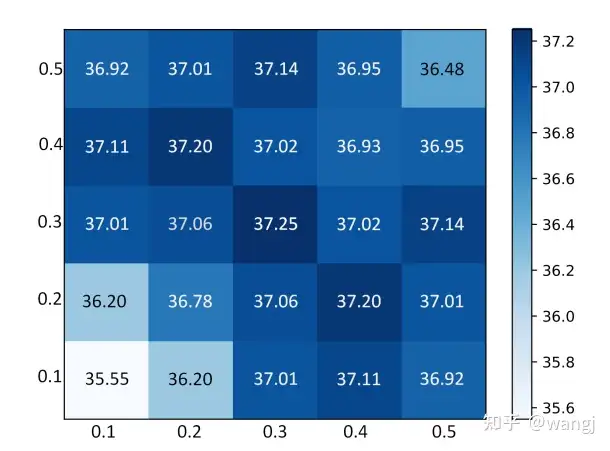
如上图所示，效果最好的两个输入的 dropout rate 都为 0.3 时，另外当两个输入的 dropout rate 都在 [0.3, 0.5] 之间时模型的效果相差不大。

当然，不同的任务，所需要的 Dropout Rate 不一定相同，可根据实际情况进行探索。

PyTorch 代码（分类问题）

参考：Github Repo: R-Drop

import torch.nn.functional as F

# define your task model, which outputs the classifier logits
model = TaskModel()

def compute_kl_loss(self, p, q, pad_mask=None):
    
    p_loss = F.kl_div(F.log_softmax(p, dim=-1), F.softmax(q, dim=-1), reduction='none')
    q_loss = F.kl_div(F.log_softmax(q, dim=-1), F.softmax(p, dim=-1), reduction='none')
    
    # pad_mask is for seq-level tasks
    if pad_mask is not None:
        p_loss.masked_fill_(pad_mask, 0.)
        q_loss.masked_fill_(pad_mask, 0.)

    # You can choose whether to use function "sum" and "mean" depending on your task
    p_loss = p_loss.sum()
    q_loss = q_loss.sum()

    loss = (p_loss + q_loss) / 2
    return loss

# keep dropout and forward twice
logits = model(x)

logits2 = model(x)

# cross entropy loss for classifier
ce_loss = 0.5 * (cross_entropy_loss(logits, label) + cross_entropy_loss(logits2, label))

kl_loss = compute_kl_loss(logits, logits2)

# carefully choose hyper-parameters
loss = ce_loss + α * kl_loss

1）KL-Divergence

使用 torch.nn.functional.kl_div() 函数。

第一个参数传入的是一个 对数概率矩阵（torch.nn.functional.log_softmax()），第二个参数传入的是 概率矩阵（torch.nn.functional.softmax()）。

这里很重要，不然求出来的 kl 散度可能是个 负值。

import torch
import torch.nn.functional as F
 
# 定义两个矩阵
x = torch.randn((4, 5))
y = torch.randn((4, 5))
 
# 因为要用y指导x,所以求x的对数概率，y的概率
logp_x = F.log_softmax(x, dim=-1)
p_y = F.softmax(y, dim=-1)
 
 
kl_sum = F.kl_div(logp_x, p_y, reduction='sum')
kl_mean = F.kl_div(logp_x, p_y, reduction='mean')
 
print(kl_sum, kl_mean)

>>> tensor(3.4165) tensor(0.1708)

非分类问题

论文 《R-Drop: Regularized Dropout for Neural Networks》 在附录 A.4 Language Understanding 中也对回归任务（非分类任务）进行了实验，使用 MSE Regularization 来作为惩罚项。

假设模型的输入为 \(x\)，两个输出结果分别为 \(y_1\) 和 \(y_2\)，ground-truth 为 \(y\)，那么最终的损失函数为：

参考

• 论文：

  • R-Drop: Regularized Dropout for Neural Networks

  • SimCSE: Simple Contrastive Learning of Sentence Embeddings

• Official Code：R-Drop

• 知乎：

  • R-Drop：提升有监督任务性能最简单的方法

  • R-Drop—-更强的正则化dropout

• 科学空间：

  • 又是Dropout两次！这次它做到了有监督任务的SOTA

  • 泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练

• CSDN：pytorch 计算 kl散度 F.kl_div()